Sensitivitet af ekspertgruppens COVID-19-modeller

Mikkel Meyer Andersen, Torben Tvedebrink
Sidst opdateret 7 min læsning Politik, Statistik

Det var med stor glæde, vi så at koden bag anbefalinger fra ekspertgruppen blev offentliggjort.

Vi er ikke med i ekspertgruppen, men vi er med i projektet omtalt her støttet af Novo Nordisk Fonden (projektnr. NNF20SA0063089).

Der er ingen tvivl om, at ekspertgruppen har gjort og stadigvæk gør et kæmpe stykke arbejde til gavn for os alle. Dette indlæg er ikke en kritik af dem eller deres arbejde. Dels vil vi påskønne åbenheden ved at benytte os af den, og dels vil vi forsøge at vise, hvor svær en opgave de er på.

Koden blev først offentliggjort på https://kagr.shinyapps.io/C19DK/ og sidenhen på https://github.com/laecdtu/C19DK (C19REST030-mappen).

Koden er til en Shiny-app, hvilket er rigtigt fint på mange måder. Det kan dog være mere besværligt at lave nogle systematiske gennemregninger hvor resultaterne gemmes og sammenlignes.

Vi har derfor lavet en R-pakke med motoren og den kan findes på https://github.com/mikldk/c19dk.

I dette indlæg vil vi se nærmere på tre af modelantagelserne og hvor følsomme resultaterne er overfor de antagelser ved at lave en sensitivitetsanalyse. Vi vil fokusere på antal indlagte på intensiv, da det er til disse data modellen tilpasses.

Vi vil kigge på følgende antagelser:

1) Residual type: Modellen kan lære fra data ved at hver Monte Carlo-kørsel (MC-kørsel) vægtes ud fra hvor godt den passer på data. Der er mange måder at udregne hvor godt en model tilnærmer sig data. Ekspertgruppen har valgt at udregne de mindste kvadraters afvigelser (forkortet MSE for mean squared error), dvs. \(\sum_i \left (y_i - \hat{y}_i \right )^2\) hvor \(i\) er dagen, \(y_i\) er det observerede antal på intensiv og \(\hat{y}_i\) er det antal på intensiv modellen forudsiger. Vi vil sammenligne det med MRSE (for mean relative squared error), dvs. \(\sum_i \left ( \log(y_i) - \log(\hat{y}_i) \right )^2\).

2) Andelen af MC-kørsler, der smides væk (fraction of bootstraps to discard): De dårligste modeller (store afvigelser mellem model og data giver lavere vægte) smides væk. Det gøres for at undgå at meget urealistiske modeller vægter for meget. Vi undersøger hvor meget denne andel betyder.

3) Fordeling af parameter forslag: I MC-kørslerne trækkes parametrene i et interval efter en ligefordeling (uniform fordeling). Vi undersøger hvad der sker, hvis man i stedet trækker det fra en normalfordeling, hvor intervaller angiver de midterste 95% af normalfordelingen (og vha. rejection sampling sikrer at der fås positive værdier)

Bemærk:

  • Modellen er den der blev anvendt til anbefalingerne i rapporten dateret 16. april 2020. Der er en nyere rapport fra 6. maj, der anvender en nyere model, der bl.a. er opdelt på regioner. Problemer er bare, at der endnu desværre mangler data, hvorfor det ikke har været muligt for os at køre den model.
  • Nedenfor er der fokuseret på Grundscenariet og med nrep = 1000 MC-kørsler.

Parametre

Nedenfor vises parametrene til forslagsfordelingerne.

Parametrene til at justere for ændringer i smittespredning efter delvis åbning af samfundet.

beta til 14 Apr - uden åbning
beta fra 14 Apr (her: grundscenarie)
Betydning Modelsymbol Nedre Øvre Betydning Modelsymbol Nedre Øvre
Smitterate indenfor <60 år aldersgruppe r.betaWIlt 0,12 0,22 Smitterate indenfor <60 år aldersgruppe r.betaWIlt1 0,16 0,26
Smitterate indenfor >=60 år aldersgruppe r.betaWIge 0,14 0,24 Smitterate indenfor >=60 år aldersgruppe r.betaWIge1 0,13 0,23
Smitterate mellem aldersgrupper r.betaB 0,02 0,12 Smitterate mellem aldersgrupper r.betaB1 0,03 0,13

Parametre som er uændrede før og efter genåbningen

Betydning Modelsymbol Nedre Øvre
MC: Skalering (“efficiency of restrictions”) r.ER 50 150
Antal dage på ICU før bortgang
Under 60 år r.mu31 14 28
Over 60 år r.mu32 14 28
Antal dage før rask udenfor hospital
Under 60 år r.recI11 4 6
Over 60 år r.recI12 4 6
Antal dage på hospital før udskrivelse
Under 60 år r.recI21 5 9
Over 60 år r.recI22 5 15
Antal dage på ICU før udskrivelse
Under 60 år r.recI31 14 28
Over 60 år r.recI32 14 28
Latenstid
Under 60 år r.kE1 4 6
Over 60 år r.kE2 4 6
Antal dage efter symptomer før indlæggelse
Under 60 år r.k1 6 10
Over 60 år r.k2 5 9
Antal dage til ICU efter indlæggelse
Under 60 år r.gI231 0,5 2,5
Over 60 år r.gI232 0,5 1,5
Andel [%] med sygdom der indlægges
Under 60 år r.pI1R1 0,05 0,5
Over 60 år r.pI1R2 5 6,2
Sandsynlighed for rask efter indlæggelse
Under 60 år r.pI2R1 0,77 0,97
Over 60 år r.pI2R2 0,7 0,9
Sandsynlighed for at overleve ICU
Under 60 år r.pI3R1 0,7 0,95
Over 60 år r.pI3R2 0,45 0,55
Antal smittede 11 marts
Under 60 år r.InfInit1 40.000 70.000
Over 60 år r.InfInit2 5.000 14.000

Data

Modellen tilpasse på grundlag af dette data:

Dato Hospital Intensiv Medtag i residualer
2020-03-11 10 0
2020-03-12 NA 0
2020-03-13 19 4
2020-03-14 NA NA
2020-03-15 26 2
2020-03-16 52 10 X
2020-03-17 64 18 X
2020-03-18 105 24 X
2020-03-19 123 30 X
2020-03-20 146 37 X
2020-03-21 164 42 X
2020-03-22 186 46 X
2020-03-23 199 55 X
2020-03-24 232 69 X
2020-03-25 263 87 X
2020-03-26 292 94 X
2020-03-27 321 109 X
2020-03-28 338 121 X
2020-03-29 368 131 X
2020-03-30 394 139 X
2020-03-31 384 145 X
2020-04-01 389 146 X
2020-04-02 372 153 X
2020-04-03 374 143 X
2020-04-04 365 142 X
2020-04-05 360 144 X
2020-04-06 364 139 X
2020-04-07 345 127 X
2020-04-08 326 127 X
2020-04-09 313 120 X
2020-04-10 288 113 X
2020-04-11 302 106 X
2020-04-12 292 104 X
2020-04-13 288 100 X

Resultater

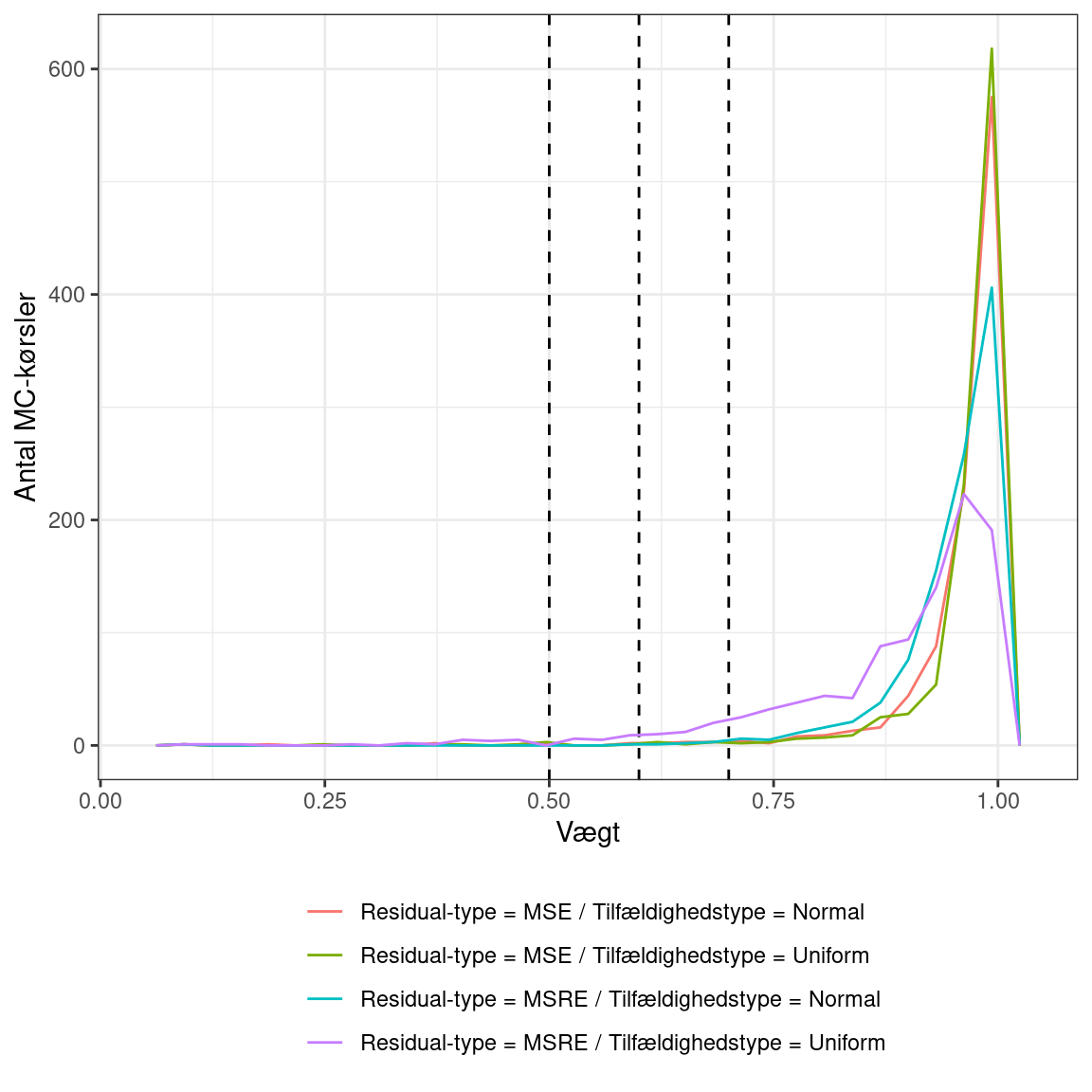
Fordeling af vægte

De lodrette streger viser de andele af ignorede MC-kørsler, der kigges nærmere på nedenfor.

Smitterater

Vi kigger også på fordelingen af de trukne smitterater fra 14. april og frem hænger sammen med vægten for modellerne. Vi fokuserer på modellerne med MSE-residualer og ligefordelte (uniforme) parametre.

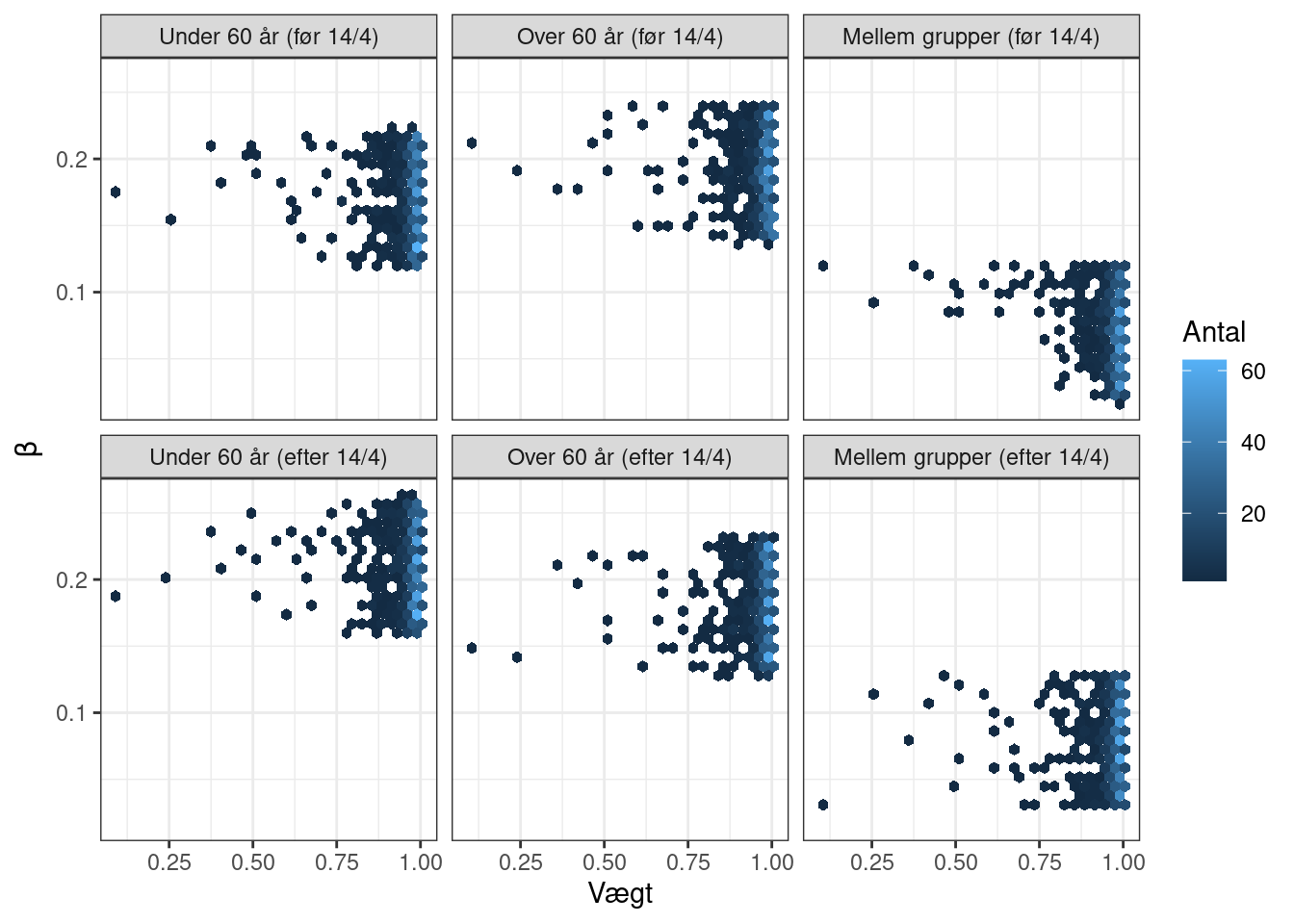
Man kan også undersøge hvordan parametrene er fordelt (korrigeret for den resulterende models vægt):

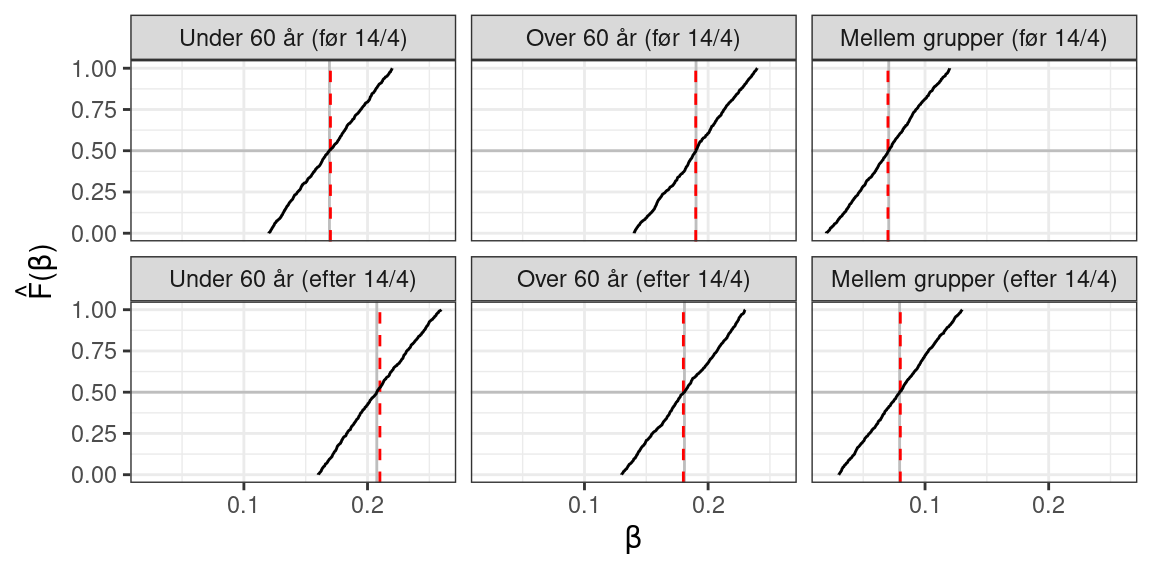
De sorte kurver er de empiriske kumulative fordelingsfunktioner. De ser alle lineære ud - altså samme type fordeling som de er trukket fra. Det kan give et hint om, at data (igennem vægtene) ikke giver meget information omkring parametrene.

De grå streger viser medianen for den fordelingen, og den røde streg viser medianen for forslagsfordelingen (se parametre længere oppe).

Som det ses ligger disse to medianer næsten oveni hinanden. Det virker altså til, at data ikke giver meget information om parametrene, og at man næsten kun ser resultatet af hvad man tror parametrene ligger imellem uden meget information fra data. Det giver også fin mening - i og med at der kun er observationer fra 29 dage til at estimere de omkring 30 parametre i modellen.

Intensivpladser

Vi kigger her på 50% fraktilen (medianen) og 90% fraktilen:

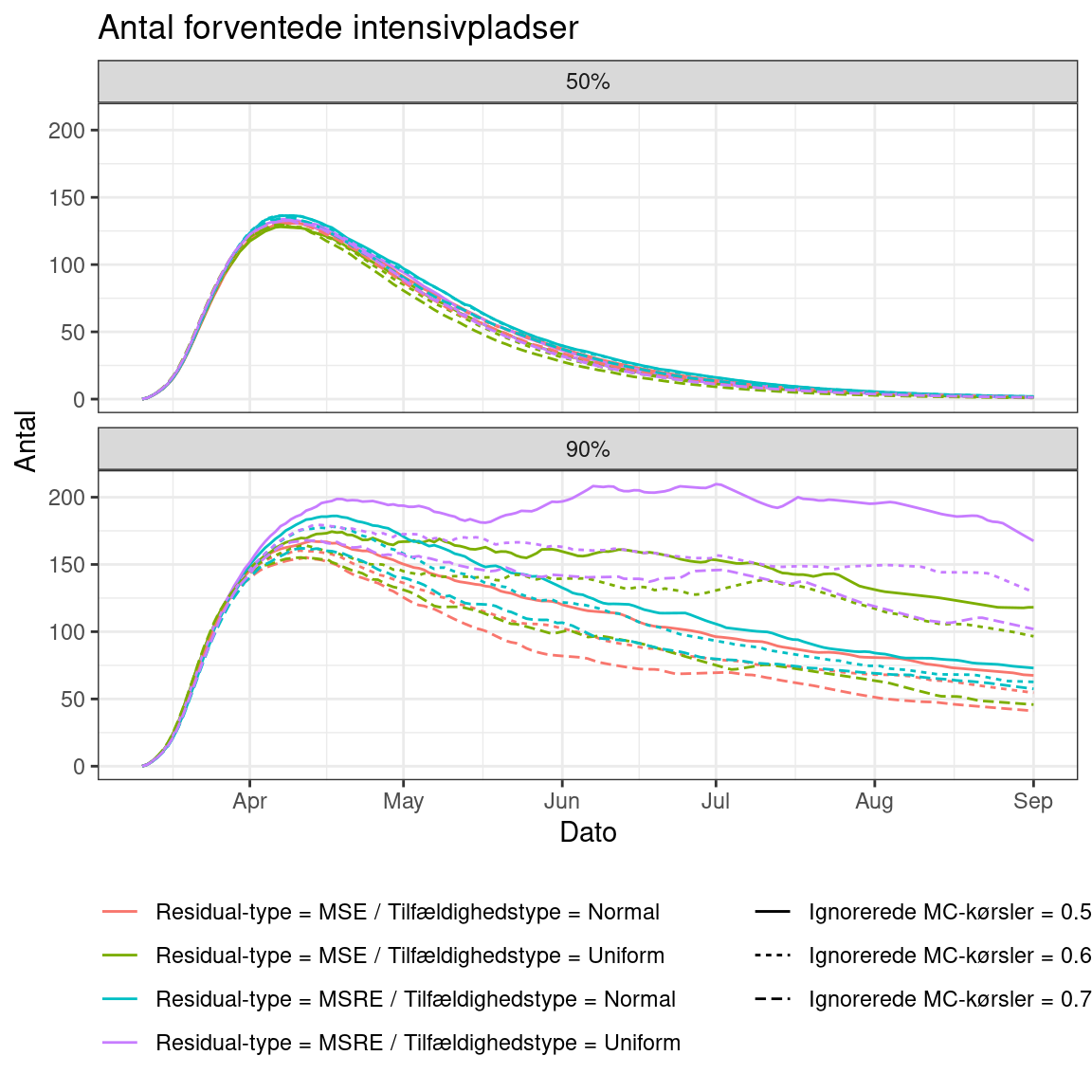
Det ses, at medianen er robust. Det ses også, at halen (90% fraktilen) er mere følsom, men det er ikke bekymrende store forskelle.

For at undersøge hvor meget data giver af information, kigger vi nu på kurverne (hvor der ignoreres 60% af MC-kørslerne) hvor alle MC-kørsler vægtes med 1:

Vi kigger her på 50% fraktilen (medianen) og 90% fraktilen:

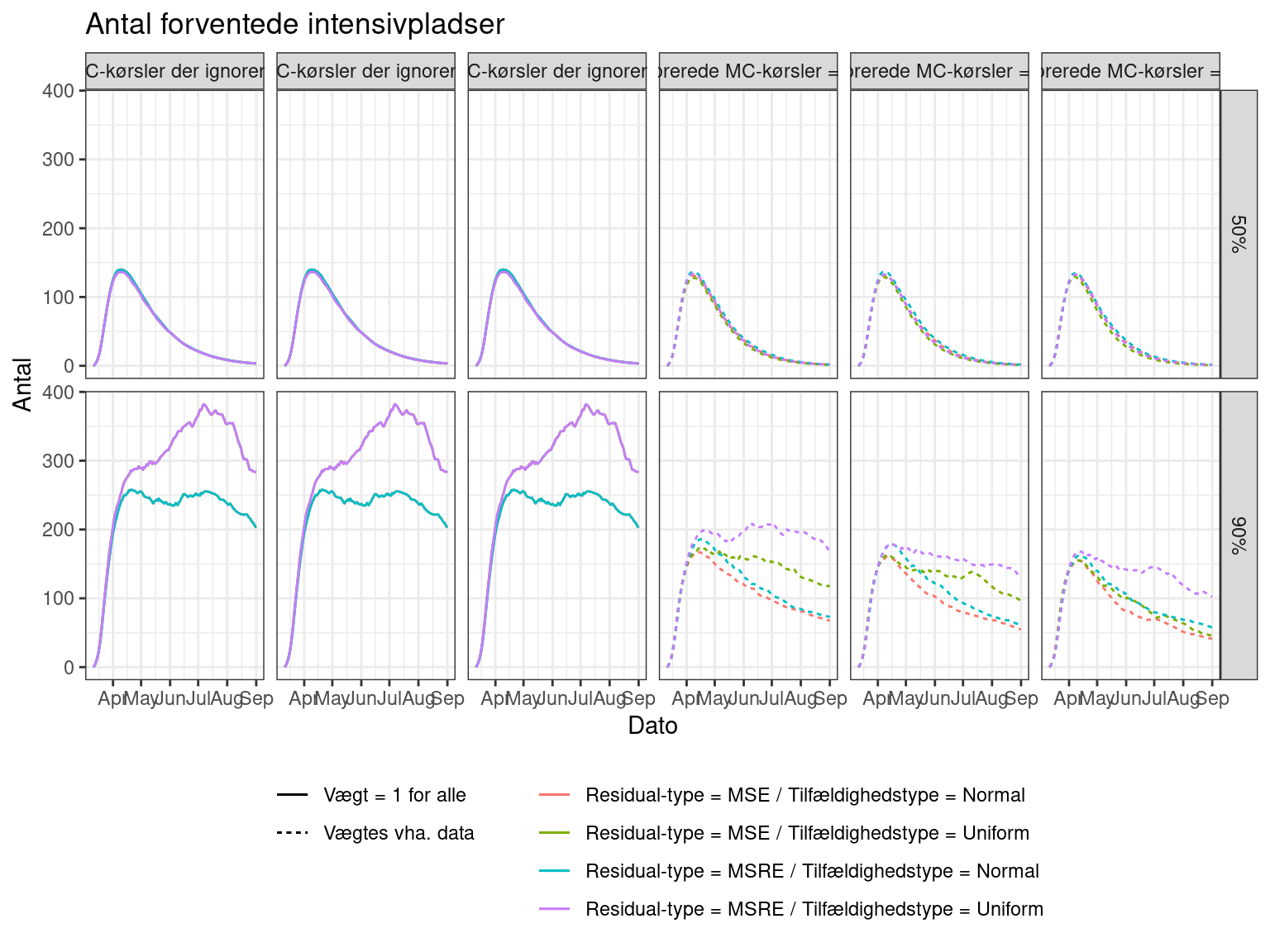
Med andre ord har data indflydelse på halerne i fordelingen (ved at fjerne ekstreme MC-kørsler), men ikke de centrale tendenser.

Hvad giver dårlige vægte?

Her anvendes den statistisk metode kaldet regressiontræer til at forsøge at forudsige en models vægt ud fra parametrene (på MSE med ligefordelte parametre).

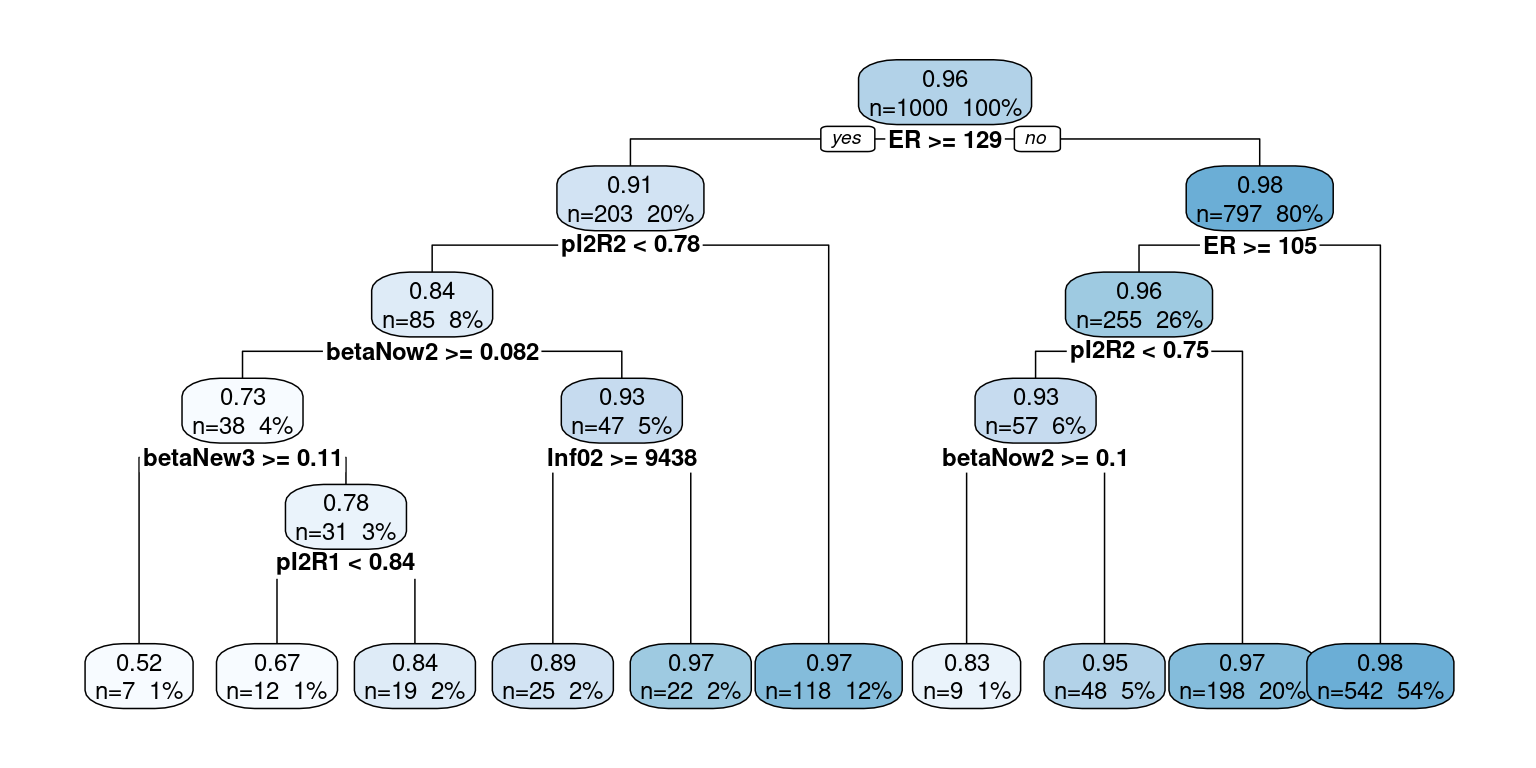
Det ses at følgende virker til at kunne sige noget om vægten:

  • ER er skalering (“efficiency of restrictions”)
  • pI2R2 er sandsynlighed for rask efter indlæggelse

De to siger dog på ingen måde alt om vægten; faktisk forklarer de kun omkring 16% af variationen i vægten (justeret \(R^2\)-værdi fra lineær regression).

Opsamling

Det er ekstremt svært at inkorporere data på fornuftig vis i modeller i SEIR-familien, og også at estimere usikkerheden. Det ser dog ikke ud til at de antagelser vi har undersøgt har en større påvirkning.

Til gengæld ser det ud til, at data ikke giver meget information om parametrene. Og usikkerheden i data er ikke inkorporeret i usikkerhedsestimaterne på kurverne (hvis 20% af befolkningen syge og man tager en stikprøve kan stikprøven vise 19%, 22% syge osv.).

At det er svært at estimere parametrene ud fra data giver også fin mening - i og med at der kun er observationer fra 29 dage til at estimere de omkring 30 parametre i modellen. Det er en problem, der er svært at gøre meget ved. En af de ting man kunne gøre, er at benytte data fra flere kurver fx (antal døde), men det er svært at sikre validiteten af de data.

Politik Statistik
Avatar
Mikkel Meyer Andersen
Lektor i anvendt statistik

Mine forskningsinteresser er bl.a. indenfor anvendt statistik og beregningsbaseret statistik.

Relaterede