I mine seneste to indlæg (“Økonomiens betydning i udbud af ny digital public service-radiokanal” og “Forventet budgets betydning i udbud af ny digital public service-radiokanal”) har jeg fokuseret på pointgivning af budgetter i udbud (nærmere bestemt “Udbud af ny digital public service-radiokanal”). I dette indlæg forklarer jeg rationalet for formlen for antallet af point, den meget omtalte lineær interpolation.
Lineær interpolation
Lineær interpolation er i sin simpleste form at finde den rette linie \(y = ax + b\) der går igennem to pointer \((x_1, y_1)\) og \((x_2, y_2)\). Når man har den rette linie kan man komme med en ny \(x\) værdi med ukendt \(y\) værdi og så finde \(y\)-værdien vha. den rette linie. Man udregner (eller estimerer) altså en \(y\) værdi baseret på de to punkter med kendte \(x\) og \(y\) værdier. Man kan lave andre former for interpolation, fx kvadratisk, splines osv. (som dog kræver flere punkter for at kunne udregne interpolationen). Omvendt kan man også lave lineær interpolation med mere end to punkter: det hedder lineær regression, og man kan så også få en usikkerhed på den estimerede \(y\) værdi.
Her fokuserer jeg på lineær interpolation ud fra to punkter, og det kan illustreret således:
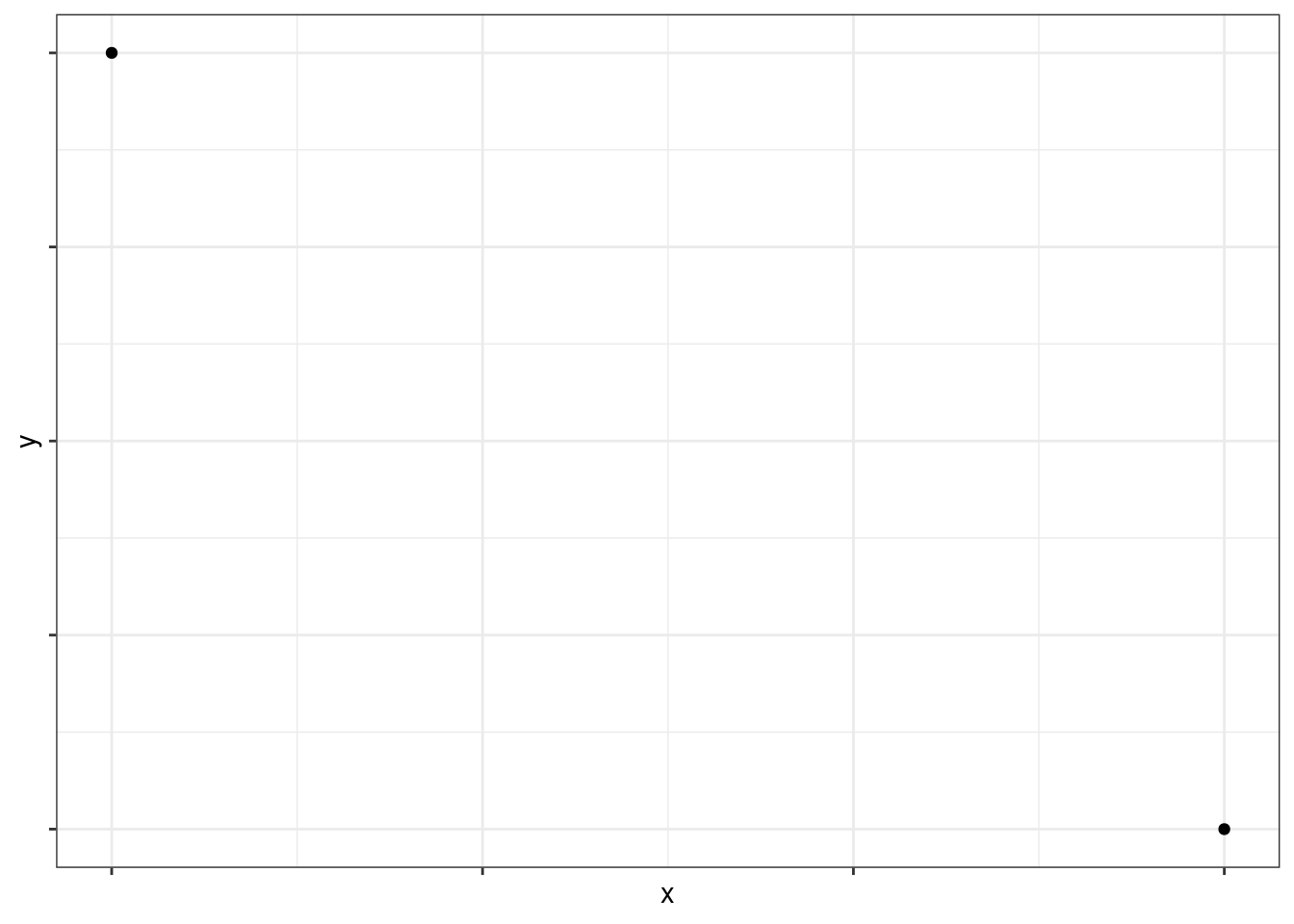
Man finder så hældningen af den rette linie, \(a\), som \[ a = \frac{\text{forskel i $y$}}{\text{forskel i $x$}} = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1} . \] Man kan også finde skæringen med \(y\)-aksen. Når \(y = ax + b\), er \[ b = y_1 - a x_1 = y_1 - \frac{y_2 - y_1}{x_2 - x_1} x_1 . \] Dermed bliver den rette linie \[\begin{align} y &= \frac{y_2 - y_1}{x_2 - x_1} x + y_1 - \frac{y_2 - y_1}{x_2 - x_1} x_1 \\ &= y_1 + \left ( \frac{y_2 - y_1}{x_2 - x_1} \right ) (x - x_1) . \end{align}\]
Dermed fremkommer den rette linie der går igennem de to punkter:
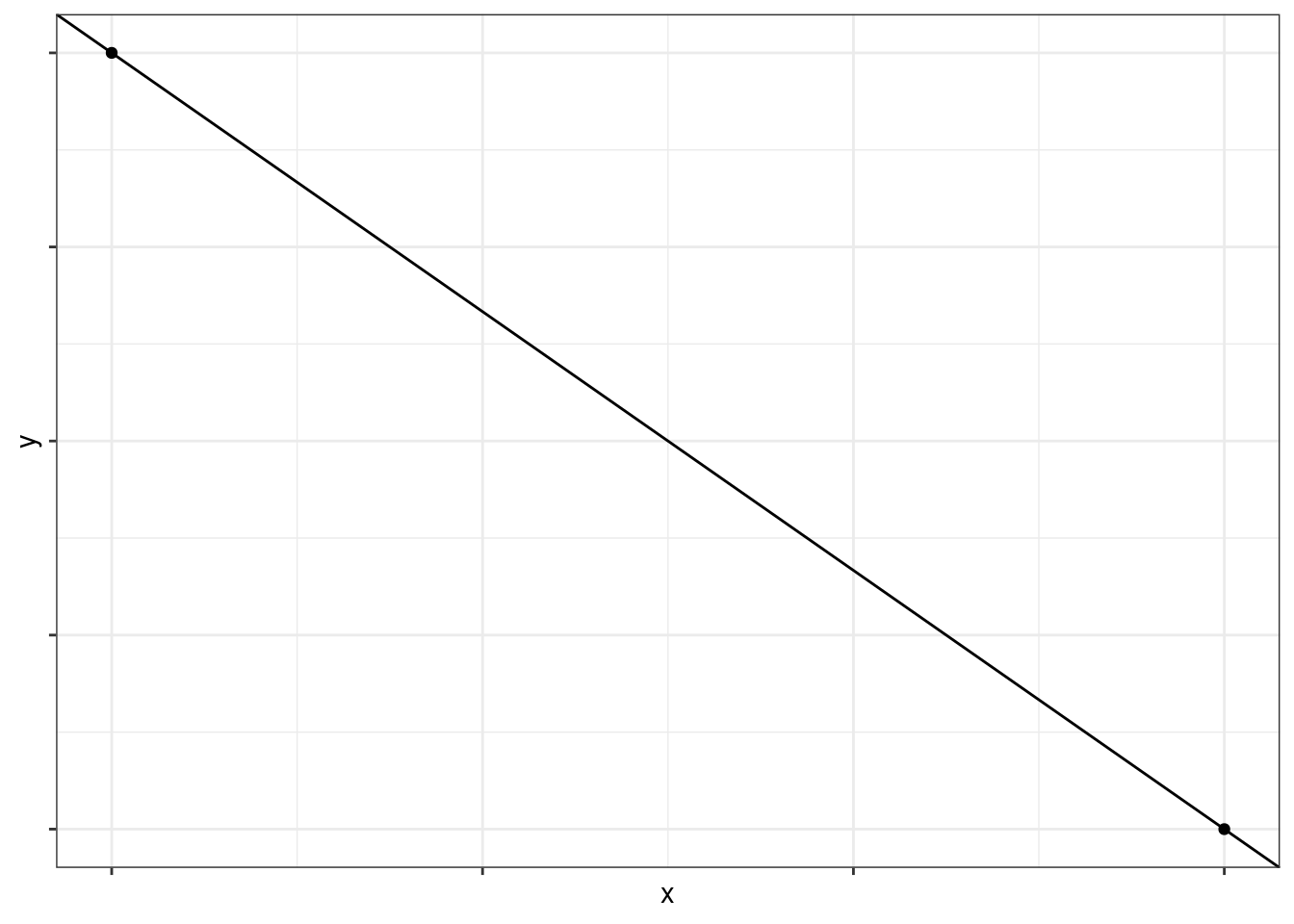
Pointgivning
Ovenfor viste jeg, hvordan man laver lineær interpolation, når man har to punkter. Nedenfor vil jeg forklare, hvordan de to punkter bestemmes i metoden beskrevet i det netop overståede “Udbud af ny digital public service-radiokanal”.
Bestemmelse af to punkter
I det netop overståede “Udbud af ny digital public service-radiokanal” skrives i evalueringsrapporten s. 24 hvordan de to punkter vælges:
Ansøgningen med det laveste ikke unormalt lave bud på tilskudssummen tildeles det højeste antal point på pointskalaen, dvs. 8 point.
Ansøgninger med et bud på en tilskudssum, der præcis svarer til laveste bud tillagt den økonomiske ramme, eller som overstiger denne sum, tildeles det mindste antal point på pointskalaen (minimumpoint) dvs. 0 point.
Så det første punkt er lige til: det mindste budget, \(s_{\text{min}}\), får \(p_{\text{max}} = 8\) point. Altså har man at \[ (x_1, y_1) = \left ( s_{\text{min}}, p_{\text{max}} \right ). \] Tilbage er “bare” at fastlægge ét punkt mere, og så kan man udregne antallet af point for de andre budgetter.
Lad os starte med at det dyreste budget, \(s_{\text{max}}\), bare får \(p_{\text{min}} = 0\) point. Altså har man det andet punkt: \[ (x_2, y_2) = \left ( s_{\text{max}}, p_{\text{min}} \right ) . \]
Nu kan vi så lave den lineære interpolation \[\begin{align} p &= p_{\text{max}} + \left ( \frac{p_{\text{min}} - p_{\text{max}}}{s_{\text{max}} - s_{\text{min}}} \right ) (s - s_{\text{min}}) , \end{align}\] hvor \(p\) er det antal point som budgettet \(s\) skal have.
Problemet er bare, at det ikke altid er fair at give det dyreste budget \(p_{\text{min}} = 0\) point. Hvad nu hvis der kun er fx 1 kr. forskel på dyreste og billigste budget? Det man i stedet gør, er at modificere punkt nummer to: med andre ord finder man et andet beløb end bare det dyreste budget, der resulterer i 0 point. I det følgende forklarer jeg hvordan det er gjort i “Udbud af ny digital public service-radiokanal”.
Den økonomiske ramme
For at have en parameter at skrue på, således man kan fastsætte det beløb der giver \(p_{\text{min}} = 0\) point har man indført et begreb man kalder den økonomiske ramme, \(s_{\text{max}}\), som er defineret som \(s_{\text{max}} = s_{\text{min}} + h s_{\text{min}}\), hvor \(s_{\text{min}}\) er det laveste bud på tilskudssummen og \(h\) kaldes hældningsgraden af den økonomiske ramme. Dermed er \[ h = \frac{s_{\text{max}} - s_{\text{min}}}{s_{\text{min}}} . \]
Den økonomiske ramme angiver at budgetter på dette beløb eller over får \(p_{\text{min}} = 0\) point. Bruger man bare det observerede budgetter får man det samme som før, men som jeg skrev, vil man typisk ikke påføre at det dyreste budget er tvunget til at få 0 point. Derfor gør man i stedet det, at man også udregner en økonomisk ramme ud fra et forventet budget som fastsættes fra dem der laver udbuddet.
Man får så to værdier af \(h\), og man kan så vælge en kombination af dem, fx gennemsnittet. Som nævnt ovenfor kan man også bare vælge én af dem, men man har altså valgt at man laver en mellemting. (Det skal sikkert afspejle, at man ikke bare vil give de dyreste 0 point, men man stoler heller ikke på det man selv fastsætter som et forventet budget. Og altså kombinerer man dem.)
Det betyder at man erstatter \(s_{\text{max}}\) med \(s_{\text{min}} + h s_{\text{min}}\), hvor \(h\) kan være bestemt på mange måder (se ovenfor), således det andet punkt hedder: \[ (x_2, y_2) = \left ( s_{\text{min}} + h s_{\text{min}}, p_{\text{min}} \right ) . \]
Nu kan vi så lave den lineære interpolation \[\begin{align} p &= p_{\text{max}} + \left ( \frac{p_{\text{min}} - p_{\text{max}}}{\left ( s_{\text{min}} + h s_{\text{min}} \right ) - s_{\text{min}}} \right ) (s - s_{\text{min}}) \\ &= p_{\text{max}} + \left ( \frac{p_{\text{min}} - p_{\text{max}}}{ h s_{\text{min}}} \right ) (s - s_{\text{min}}) \\ &= p_{\text{max}} - \left ( \frac{p_{\text{max}} - p_{\text{min}}}{ h s_{\text{min}}} \right ) (s - s_{\text{min}}) \\ &= p_{\text{max}} - \left ( \frac{p_{\text{max}} - p_{\text{min}}}{ h } \right ) \left (\frac{s - s_{\text{min}}}{s_{\text{min}}} \right ) , \end{align}\] hvor \(p\) er det antal point som budgettet \(s\) skal have. Og det er præcis den formel der står på s. 24 i evalueringsrapporten.
Opsummering
Som beskrevet ovenfor har man valgt at det billigste budget skal have det maksimale antal point. Man har også valgt (med god grund), at det dyreste budget ikke bare skal have det minimale antal point. For så at finde det beløb, der skal have det minimale antal point, introducerer man en hældningsgrad som fastsættes. Hvis den bare blev fastsat ud fra de indkomne bud, ville man være tilbage ved start, hvor det dyreste bud ville få det minimale antal point. Derfor laver man en forventet budgetramme og udregner en hældningsgrad her. De to hældningsgrader bruger man så for at komme frem til det beløb, der skal have det minimale antal point.
I evalueringsrapporten for “Udbud af ny digital public service-radiokanal” kan man på s. 25 finde budgetterne. Der kommer man frem til en observeret hældningsgrad på 9.27% og en forventet hældningsgrad på 12%. De kombineres så (på en ikke nærmere beskrevet måde) til et interval af hældningsgrad på 10-11%. Det kan man så omregne til hvornår man giver budgetter 0 point (“den økonomiske ramme”). For en hældningsgrad på 10% bliver den økonomiske ramme \(256.25 + 0.1 \cdot 256.25\) mio. = \(281.88\) mio. og for en hældningsgrad på 11% bliver den økonomiske ramme \(256.25 + 0.11 \cdot 256.25\) mio. = \(284.44\) mio.
Diskussion
Ovenstående lægger op til det overordnede politiske spørgsmål om lineær interpolation med en hældningsgrad bestemt som beskrevet ovenfor er en fornuftig model at bruge, når der er afsat en økonomisk ramme (og dermed en øvre grænse).
Man kan lave rigtig mange modeller til sådan noget her, og det skal være gennemsigtigt og operationelt. Et alternativ kunne være at man i stedet i udbuddet havde skrevet, at man fik 4 point (“Tilfredsstillende”) for at søge de maksimale beløb, og ellers 1 point ekstra per (ca.) 5 mio. man kunne gøre det billigere (fx 5 point for 270-275 mio., 6 point for 265-269 mio., 7 point for 260-264 mio. og 8 point for 255-259 mio.). Og naturligvis 0 point for over 280 mio. Det ville gøre pointgivningen langt mere gennemskuelig, og samtidig både gøre det acceptabelt at søge om den maksimale ramme og belønne billigere forslag.