Som opfølgning på et tidligere indlæg omkring “Udbud af ny digital public service-radiokanal”
undersøger jeg her, hvilken betydning det forventede minimumsbudget har for hældningen og dermed for de vægtede point for det ansøgte beløb.
Bemærk at hældningen afgør udelukkende den indbyrdes fordeling af point. Den ændrer ikke på rangordningen.
Jeg undersøger også hvilken betydning det har om man afrundet før eller efter vægtningen.
Til sidst i indlægget kan du finde R-koden til at reproducere min analyse.
I udbudsmaterialet nævnes der ikke et interval for de forventede bud. I evalueringsrapporten s. 25 skrives
Ud fra en samlet betragtning med udgangspunkt i ovenstående forventes tilskudssummerne derfor at falde indenfor intervallet 250 mio. kr.-280 mio. kr., hvilket vil give en hældningsgrad på 12 pct. Den faktiske spredning af tilbuddene havde en afrundet hældningsgrad på 9 pct.
Da der er krav om at tage hensyn til både den faktiske og den forventede spredning erhældningsgraden, som er anvendt til beregningen af pointpå denne baggrund fastsat til at ligge i intervallet 10-11 pct.
Det er uklart hvordan de 250 mio. kr. er blevet bestemt. Her undersøger jeg, hvad der ville ske, hvis intervallet ikke hedder 250-280 mio. men i stedet noget andet. Jeg holder fast i maksimum, og ændrer kun på det forventede minimum. For at kunne udregne konsekvenserne, skal man antage hvordan den forventede hældning kombineres med den faktiske hældning. Her antager jeg et simpelt (aritmetisk) gennemsnit.
For at opsummere:
- Den forventede hældning er .
- Den observerede hældning er .
- Det aritmetiske gennemsnit af de to er 0.106
Hvad sker der hvis det forventede budget ændrede sig?
For forventede minimumsbudgetter ses at det aritmetiske gennemsnit på hældningen mellem det forventede og observerede er:
| Min. forventet budget | Hældning forv. | Hældning (komb. forv. og obs.) |
|---|---|---|
| 150 | 0.867 | 0.480 |
| 175 | 0.600 | 0.346 |
| 200 | 0.400 | 0.246 |
| 225 | 0.244 | 0.169 |
| 250 | 0.120 | 0.106 |
| 275 | 0.018 | 0.055 |
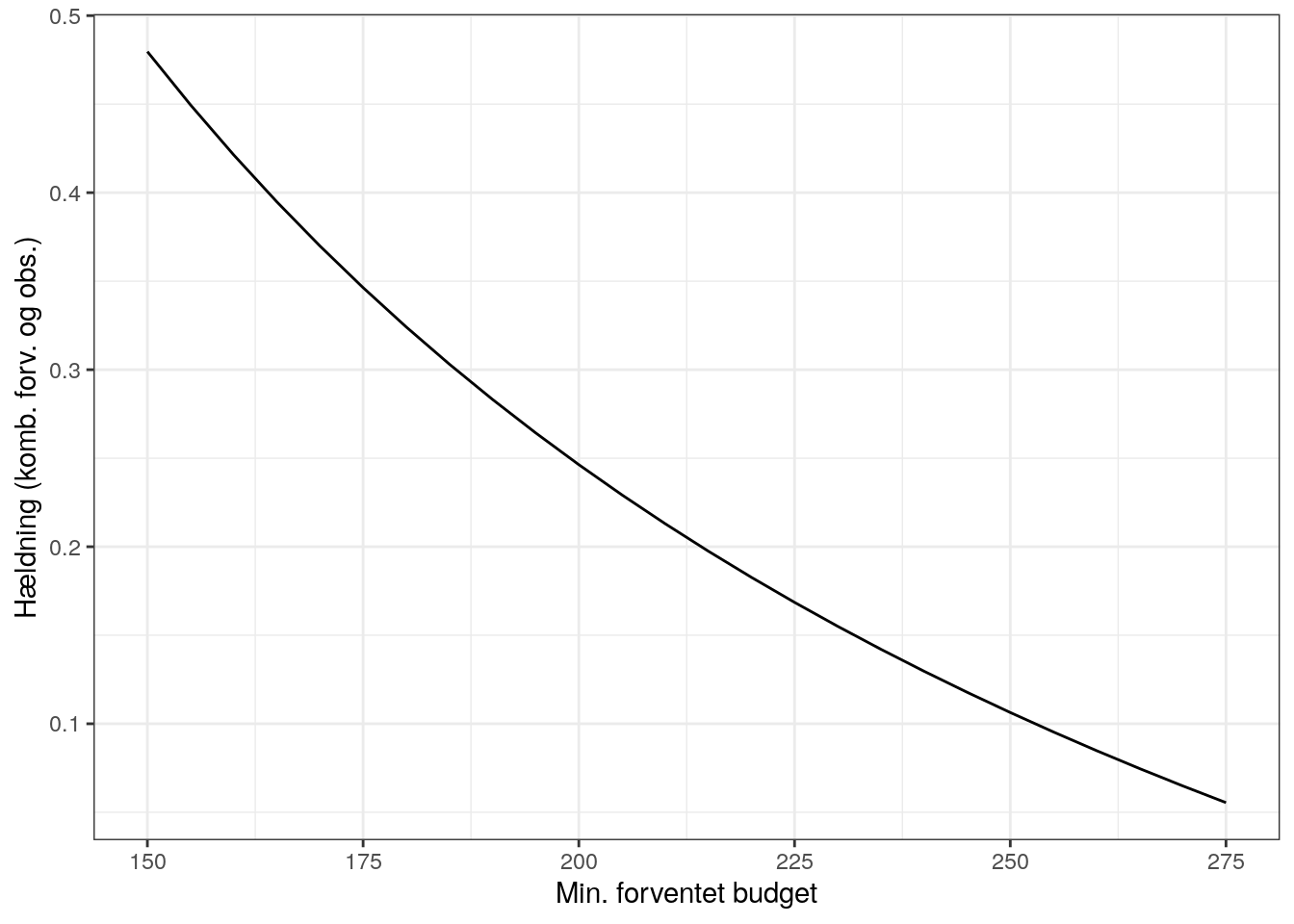
Bruger man disse hældninger får man følgende resultat, hvor vægtet er de afrundede ganget med 0,25:
| Min. forventet budget | DK4 | LOUD | R24syv | DK4 | LOUD | R24syv | DK4 | LOUD | R24syv |
|---|---|---|---|---|---|---|---|---|---|
| 150 | 8 | 7.70 | 6.45 | 2 | 2.00 | 1.50 | 2 | 2 | 2 |
| 175 | 8 | 7.59 | 5.86 | 2 | 2.00 | 1.50 | 2 | 2 | 1 |
| 200 | 8 | 7.42 | 4.99 | 2 | 1.75 | 1.25 | 2 | 2 | 1 |
| 225 | 8 | 7.15 | 3.60 | 2 | 1.75 | 1.00 | 2 | 2 | 1 |
| 245 | 8 | 6.79 | 1.70 | 2 | 1.75 | 0.50 | 2 | 2 | 0 |
| 250 | 8 | 6.66 | 1.03 | 2 | 1.75 | 0.25 | 2 | 2 | 0 |
| 255 | 8 | 6.51 | 0.22 | 2 | 1.75 | 0.00 | 2 | 2 | 0 |
| 275 | 8 | 5.43 | 0.00 | 2 | 1.25 | 0.00 | 2 | 1 | 0 |
Ovenfor er “Point: afrundet så vægtet” fremhævet da det er sådan evalueringen er foretaget- Bemærk at point under 0 er sat til 0. Det er i sig selv et punkt som hverken udbudsmaterialet eller evalueringsrapporten beskriver hvordan man kan håndtere. Der bruges dog en skale på 0-8 point, så jeg har valgt at fortolke det sådan at negative point vil få tildelt 0 i stedet for at få fratrukket point.
Udregner man det for minimum forventede budgetter i små forøgelser på 5 mio. kan man lave en illustration:
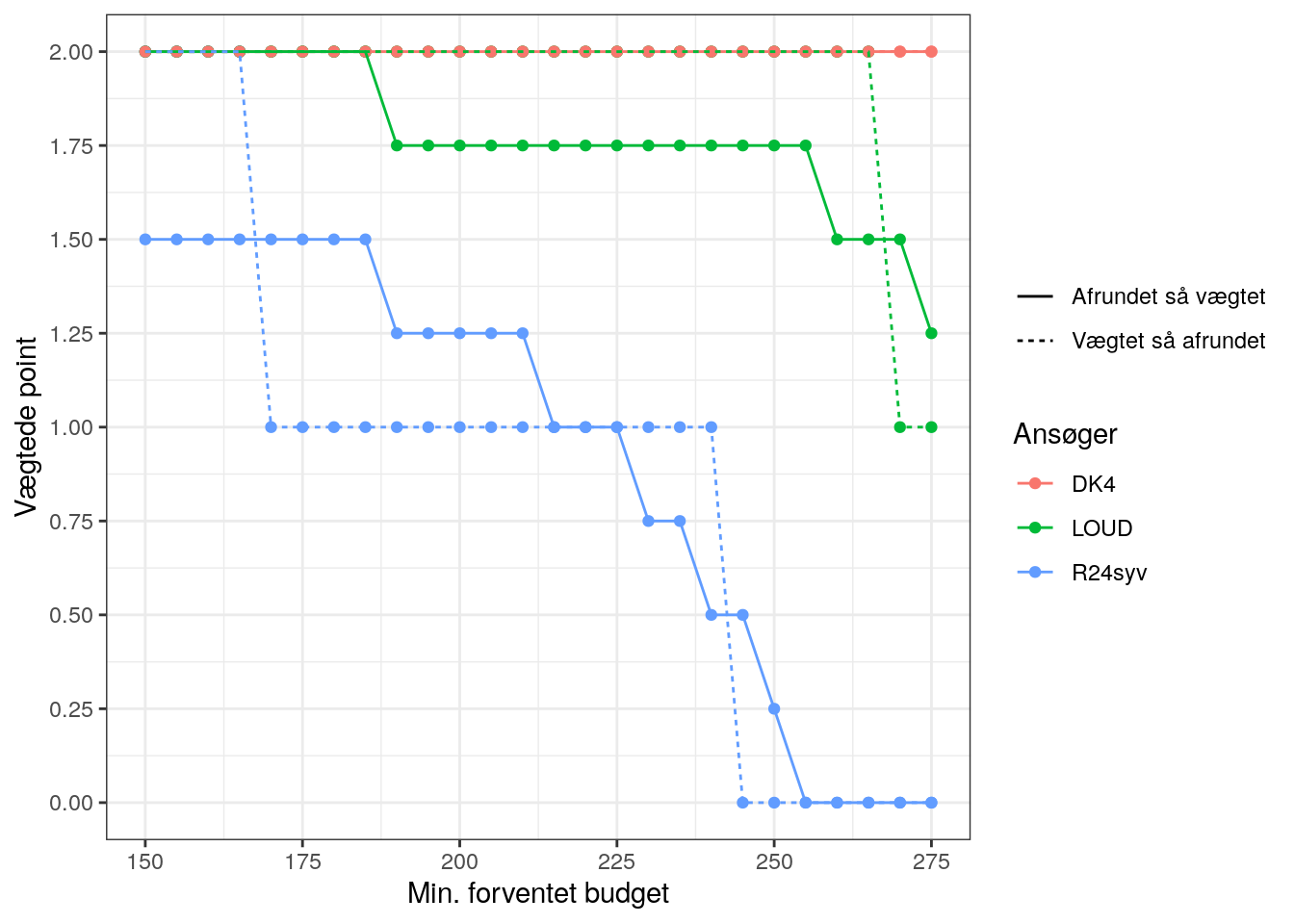
Konklusion
Som det ses afhænger metoden både af den mindste forventede budget samt hvornår man afrunder. Hvis man for eksempel havde forventet et minimumsbudget på 225 mio. (i stedet for 250 mio.), ville Radio24syv have fået 1 vægtet point i stedet for 0,25 vægtet point.
Bilag: R-kode
Ovenstående er baseret på følgende kode:
library(knitr)
library(kableExtra)
library(tidyverse)
theme_set(theme_bw())
s_ans <- c("R24syv" = 280000000,
"LOUD" = 260815062,
"DK4" = 256250000)
p_max <- 8
p_min <- 0
s_min <- min(s_ans)
s_max <- max(s_ans)
sd_obs <- (s_max - s_min)/s_min
sd_exp_max <- 280
sd_exp_min <- 250
sd_exp <- (sd_exp_max - sd_exp_min)/sd_exp_min
sd_mean_ari <- mean(c(sd_obs, sd_exp))
sd_mean_geo <- sqrt(prod(c(sd_obs, sd_exp)))
get_slope <- function(sd_exp_min) {
sd_exp <- (sd_exp_max - sd_exp_min)/sd_exp_min
sd_mean_ari <- mean(c(sd_obs, sd_exp))
return(tibble(`Hældning forv.` = sd_exp,
`Hældning (komb. forv. og obs.)` = sd_mean_ari))
}
lin_int <- function(a) {
p_max - ((p_max - p_min)/a)*(s_ans - s_min)/s_min
}
d_slope <- tibble(`Min. forventet budget` = list(seq(150, 275, by = 5))) %>%
unnest() %>%
rowwise() %>%
mutate(Hældning = list(get_slope(`Min. forventet budget`))) %>%
unnest()
d_slope %>%
filter(`Min. forventet budget` %in% c(150, 175, 200, 225, 250, 275)) %>%
knitr::kable()
ggplot(d_slope, aes(`Min. forventet budget`, `Hældning (komb. forv. og obs.)`)) +
geom_line()
d_pt <- d_slope %>%
rowwise() %>%
mutate(pt = list(enframe(lin_int(a = `Hældning (komb. forv. og obs.)`), name = "Ansøger", value = "Point"))) %>%
unnest() %>%
mutate(Point = ifelse(Point < 0, 0, Point)) %>%
mutate(`Point afrundet -> vægtet` = 0.25*round(Point)) %>%
mutate(`Point vægtet -> afrundet` = round(0.25*Point)) %>%
mutate(point_txt = paste0(round(Point, 2), " / ",
`Point afrundet -> vægtet`, " / ",
`Point vægtet -> afrundet`))
d_tab_raw <- d_pt %>%
filter(`Min. forventet budget` %in% c(150, 175, 200, 225, 245, 250, 255, 275)) %>%
select(`Min. forventet budget`, Ansøger, Point, `Point afrundet -> vægtet`, `Point vægtet -> afrundet`) %>%
gather(Type, Point, c(Point, `Point afrundet -> vægtet`, `Point vægtet -> afrundet`)) %>%
mutate(Type = case_when(
Type == "Point afrundet -> vægtet" ~ "Point: afrundet så vægtet",
Type == "Point vægtet -> afrundet" ~ "Point: vægtet så afrundet",
TRUE ~ Type
)) %>%
unite(Budget_type, Type, Ansøger) %>%
spread(Budget_type, Point)
d_tab_raw_select_order <- c(1,
which(grepl("Point_", colnames(d_tab_raw))),
which(grepl("Point: afrundet så vægtet_", colnames(d_tab_raw))),
which(grepl("Point: vægtet så afrundet", colnames(d_tab_raw))))
d_tab_raw <- d_tab_raw %>%
select(!!d_tab_raw_select_order)
sts <- gsub("^(.*)_.*$", "\\1", colnames(d_tab_raw)[-1])
sts_rle <- rle(sts)
sts_rle_cs <- cumsum(sts_rle$lengths)
header <- c(1, sts_rle$lengths)
names(header) <- c(" ", sts_rle$values)
d_tab <- d_tab_raw %>%
rename_all(list(~ gsub("^.*_(.*)$", "\\1", .)))
d_tab %>%
knitr::kable(digits = 2) %>%
kableExtra::add_header_above(header) %>%
kableExtra::column_spec(sts_rle_cs - 1, border_left = TRUE) %>%
kableExtra::column_spec(1+((sts_rle_cs[1]+1):(sts_rle_cs[2])), background = "#FF999933")
d_pt_tmp <- d_pt %>%
select(`Min. forventet budget`, Ansøger, `Point afrundet -> vægtet`, `Point vægtet -> afrundet`) %>%
gather(Type, `Vægtede point`, `Point afrundet -> vægtet`, `Point vægtet -> afrundet`) %>%
mutate(Type = case_when(
Type == "Point afrundet -> vægtet" ~ "Afrundet så vægtet",
Type == "Point vægtet -> afrundet" ~ "Vægtet så afrundet"
))
ggplot(d_pt_tmp, aes(`Min. forventet budget`, `Vægtede point`, color = Ansøger, linetype = Type)) +
geom_point() +
geom_line() +
scale_linetype_discrete(NULL) +
scale_y_continuous(breaks = seq(0, 2, by = 0.25))