Prediction intervals for Generalized Additive Models (GAMs)

Update on Aug 9, 2022: In the code chunk below, sd = summary(fit_gam)$scale) was changed to sd = sqrt(summary(fit_gam)$scale)):

y_sim <- matrix(rnorm(n = prod(dim(exp_val_sim)), 
                     mean = exp_val_sim, 
                     sd = summary(fit_gam)$scale), 
               nrow = nrow(exp_val_sim), 
               ncol = ncol(exp_val_sim))

Thanks to David Kaplan (IRD, France)

Finding prediction intervals (for future observations) is something different than finding confidence intervals (for unknown population parameters).

Here, I demonstrate one approach to doing so.

First we load the library and simulate some data:

library(mgcv)
set.seed(1)
dat <- gamSim(eg = 1, n = 400, dist = "normal", scale = 2)
## Gu & Wahba 4 term additive model

The simulated in dat contains the “truth” in the f variables:

str(dat)
## 'data.frame':    400 obs. of  10 variables:
##  $ y : num  3.3407 -0.0758 10.6832 8.7291 14.9911 ...
##  $ x0: num  0.266 0.372 0.573 0.908 0.202 ...
##  $ x1: num  0.659 0.185 0.954 0.898 0.944 ...
##  $ x2: num  0.8587 0.0344 0.971 0.7451 0.2733 ...
##  $ x3: num  0.367 0.741 0.934 0.673 0.701 ...
##  $ f : num  5.51 3.58 8.69 8.75 16.19 ...
##  $ f0: num  1.481 1.841 1.948 0.569 1.184 ...
##  $ f1: num  3.74 1.45 6.74 6.02 6.6 ...
##  $ f2: num  2.98e-01 2.88e-01 8.61e-05 2.16 8.40 ...
##  $ f3: num  0 0 0 0 0 0 0 0 0 0 ...
fit_lm <- lm(f ~ f0 + f1 + f2 + f3, data = dat)
plot(dat$f, predict(fit_lm))
abline(0, 1)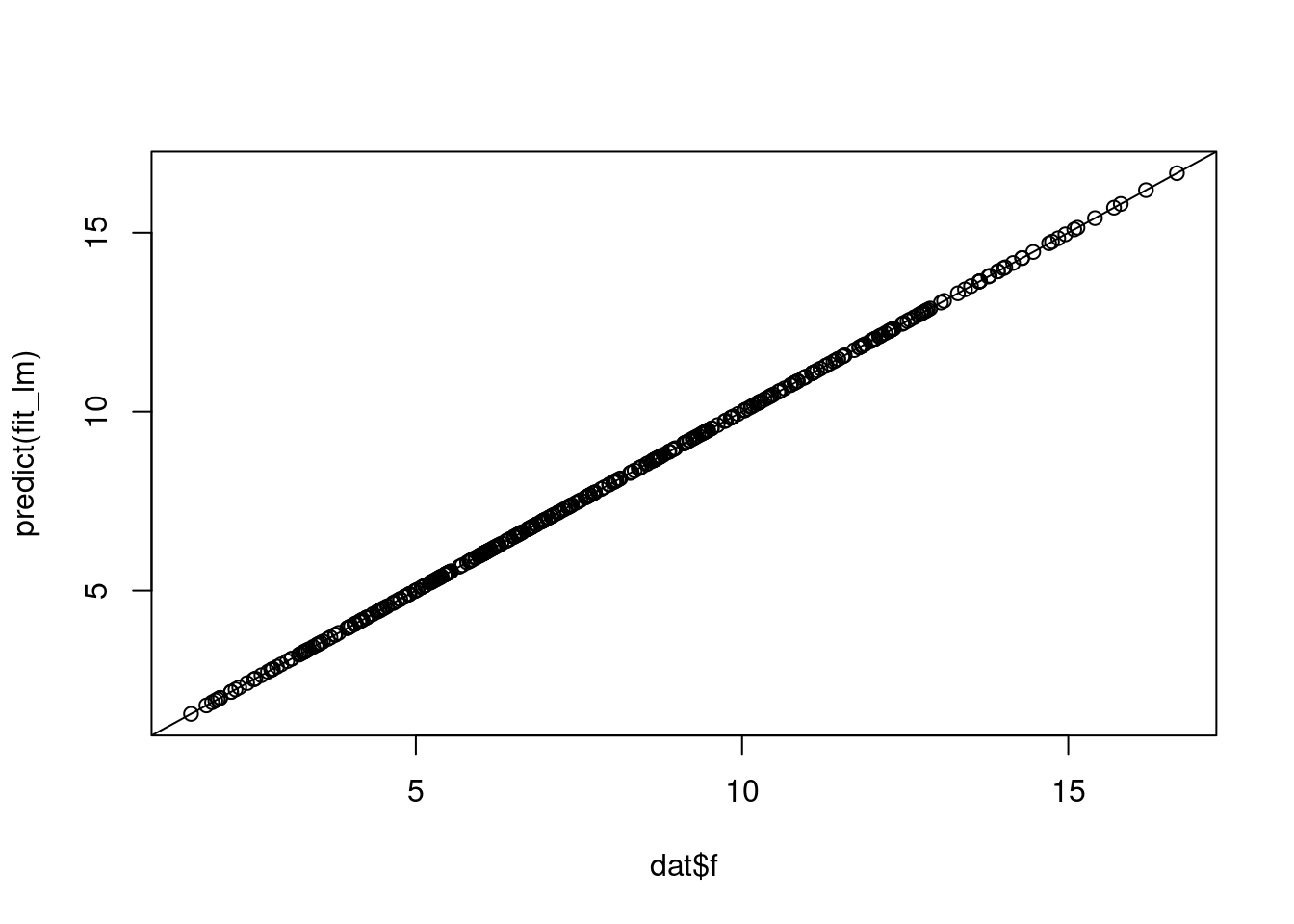

And what can be used to demonstrate GAMs are available in the y and x variables:

fit_gam <- gam(y ~ s(x0) + s(x1) + s(x2) + s(x3), data = dat)

The idea is to simulate parameter vectors, and using such a simulated parameter vector, we can draw observations. Doing this many times can be used to generate a prediction interval.

We first extract the parameter estimates and their covariance matrix:

beta <- coef(fit_gam)
V <- vcov(fit_gam)

We then to simulate a number of parameter vectors. This is done by assuming approximate normality and using the Cholesky trick. The trick is that \[ \hat{\beta} + L \nu \quad \dot \sim \quad \text{MultivariateNormal}(\beta, V) , \] where \(V = L L^\top\) is the Cholesky factorisation of the covariance matrix \(V\) and \(\nu \sim N(0, 1)\).

num_beta_vecs <- 10000
Cv <- chol(V)
set.seed(1)
nus <- rnorm(num_beta_vecs * length(beta))
beta_sims <- beta + t(Cv) %*% matrix(nus, nrow = length(beta), ncol = num_beta_vecs)
dim(beta_sims)
## [1]    37 10000

This should give us something similar to the confidence intervals of the model fit:

d_beta <- cbind(summary(fit_gam)$se, apply(beta_sims, 1, sd))
head(d_beta)
##                  [,1]      [,2]
## (Intercept) 0.1036817 0.1039225
## s(x0).1     0.3977579 0.3988932
## s(x0).2     0.7249847 0.7212706
## s(x0).3     0.1967577 0.1982036
## s(x0).4     0.4260063 0.4265382
## s(x0).5     0.1450504 0.1444811
plot(d_beta[, 1], d_beta[, 2], 
     xlab = "Calculated SE", 
     ylab = "Simulated SE")
abline(0, 1)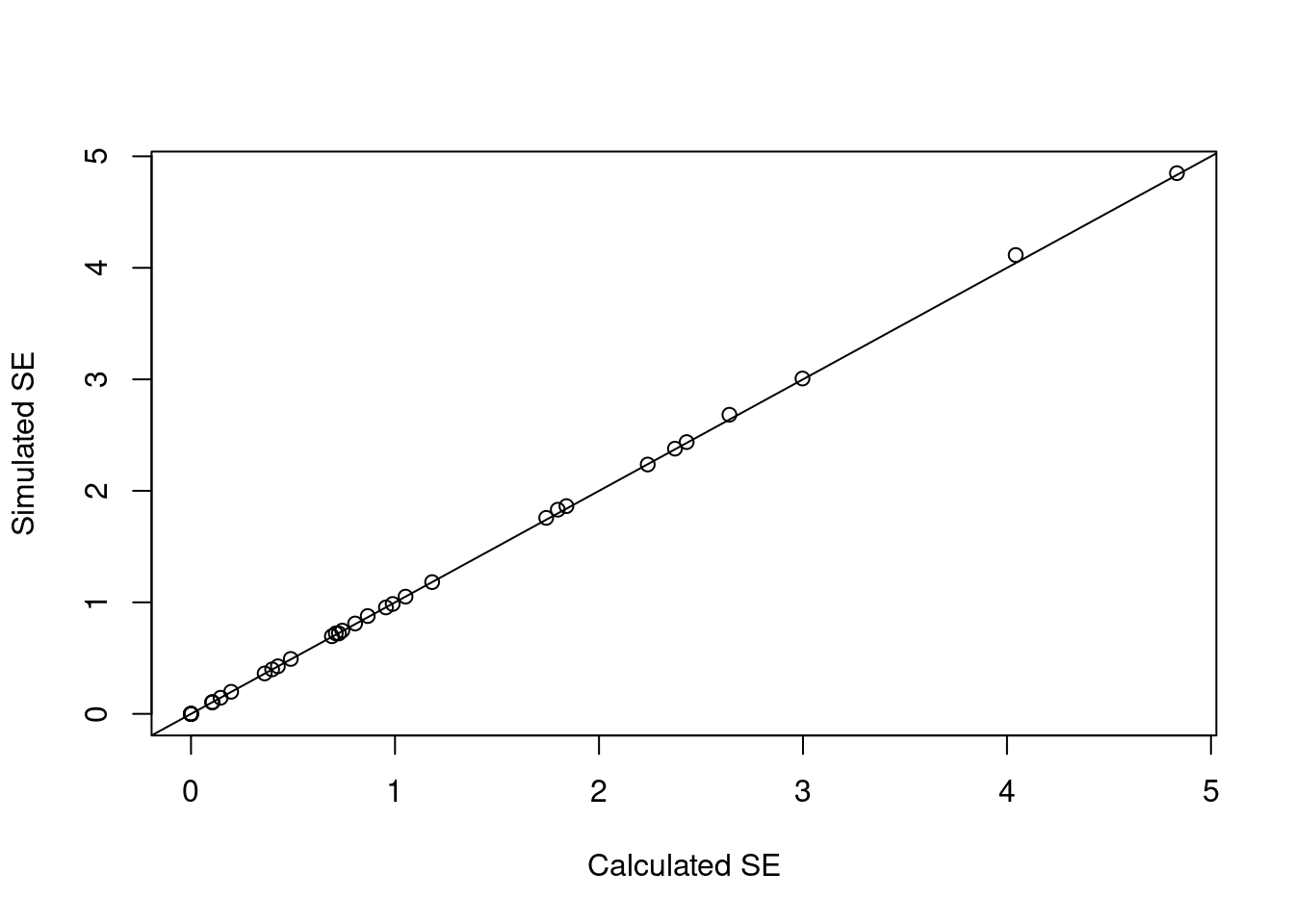

We can now proceed to simulating observations. We do that by randomly sampling from the observations with replacement:

n_obs <- 100
sim_idx <- sample.int(nrow(dat), size = n_obs, replace = TRUE)
sim_dat <- dat[sim_idx, c("x0", "x1", "x2", "x3")]
dim(sim_dat)
## [1] 100   4
# sim_dat <- dat[, c("x0", "x1", "x2", "x3")]
# dim(sim_dat)

Instead of doing such a sampling, it is also possible to use e.g. a grid of values:

if (FALSE) { # Intentionally not run
  xs_range <- apply(dat[, c("x0", "x1", "x2", "x3")], 2, range)
  xs_seq <- apply(xs_range, 2, function(x) seq(from = x[1], to = x[2], length.out = 10))
  xs_seq_lst <- as.list(as.data.frame(xs_seq))
  sim_dat <- do.call(expand.grid, list(xs_seq_lst, KEEP.OUT.ATTRS = FALSE))
  dim(sim_dat)
}

Now we can calculate the linear predictors:

covar_sim <- predict(fit_gam, newdata = sim_dat, type = "lpmatrix")
linpred_sim <- covar_sim %*% beta_sims

Now, the inverse link function must be applied to obtain the expected values. So if e.g. family = Gamma(link = log) was used in gam(), then exp() must be used. We used the Gaussian family with identity link so the inverse is the identity:

invlink <- function(x) x
exp_val_sim <- invlink(linpred_sim)

Now, the family itself must be used. If Gamma was used, then rgamma() (properly parametised) must be used. We just used Gaussian, so:

y_sim <- matrix(rnorm(n = prod(dim(exp_val_sim)), 
                      mean = exp_val_sim, 
                      sd = sqrt(summary(fit_gam)$scale)), 
                nrow = nrow(exp_val_sim), 
                ncol = ncol(exp_val_sim))
dim(y_sim)
## [1]   100 10000

So now entry \((i, j)\) of y_sim contains the \(i\)’th simulated observation’s simulated response under parameter vector \(j\) (column \(j\) of beta_sims).

We can then find a 95% prediction interval:

pred_int_sim <- apply(y_sim, 1, quantile, prob = c(.025, 0.975))
dim(pred_int_sim)
## [1]   2 100

And e.g. plot it against x0:

plot(y ~ x0, data = dat)

sim_dat_x0ord <- order(sim_dat$x0)
lines(sim_dat$x0[sim_dat_x0ord], pred_int_sim[1L, sim_dat_x0ord], col = 2, lwd = 2)
lines(sim_dat$x0[sim_dat_x0ord], pred_int_sim[2L, sim_dat_x0ord], col = 2, lwd = 2)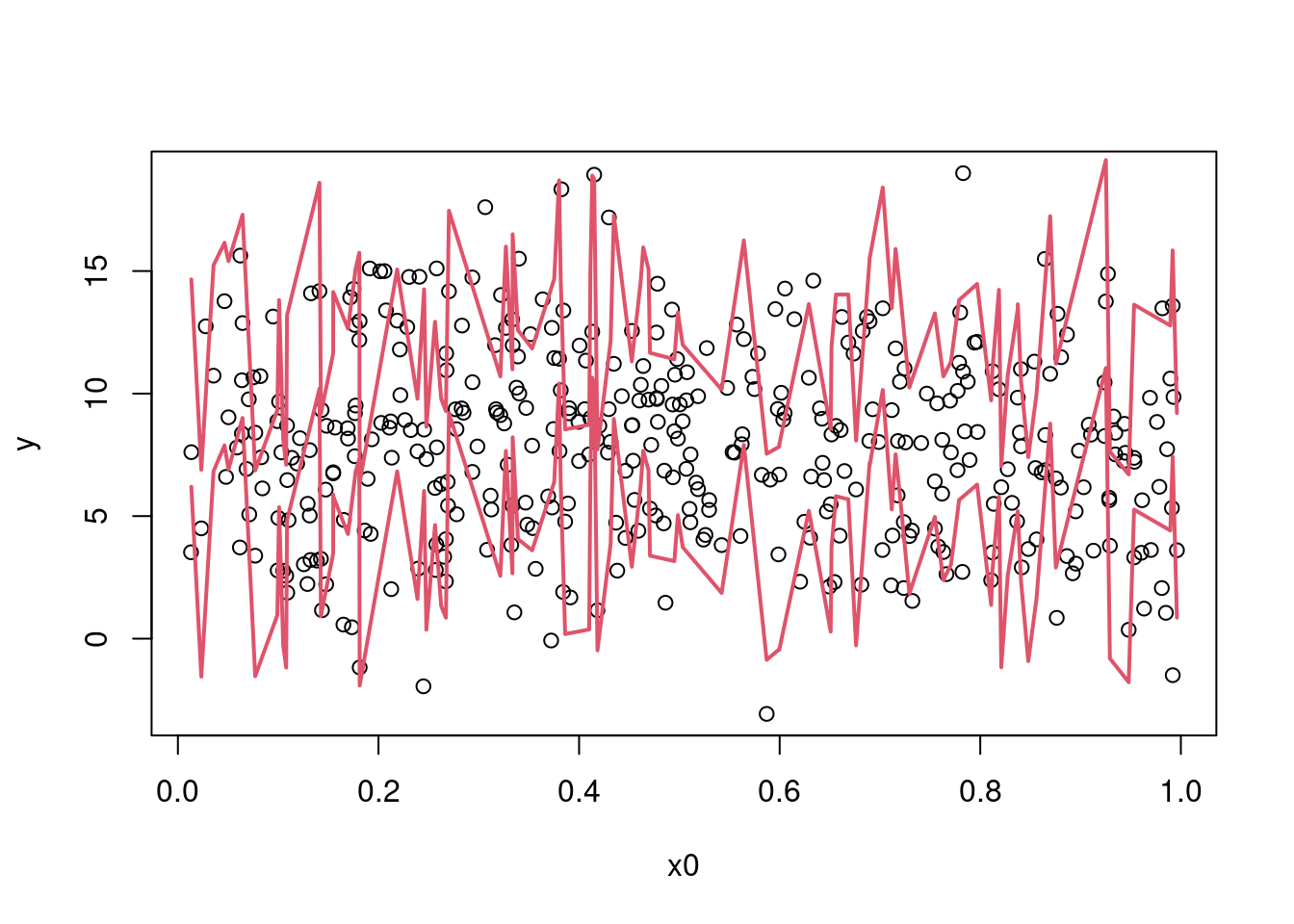

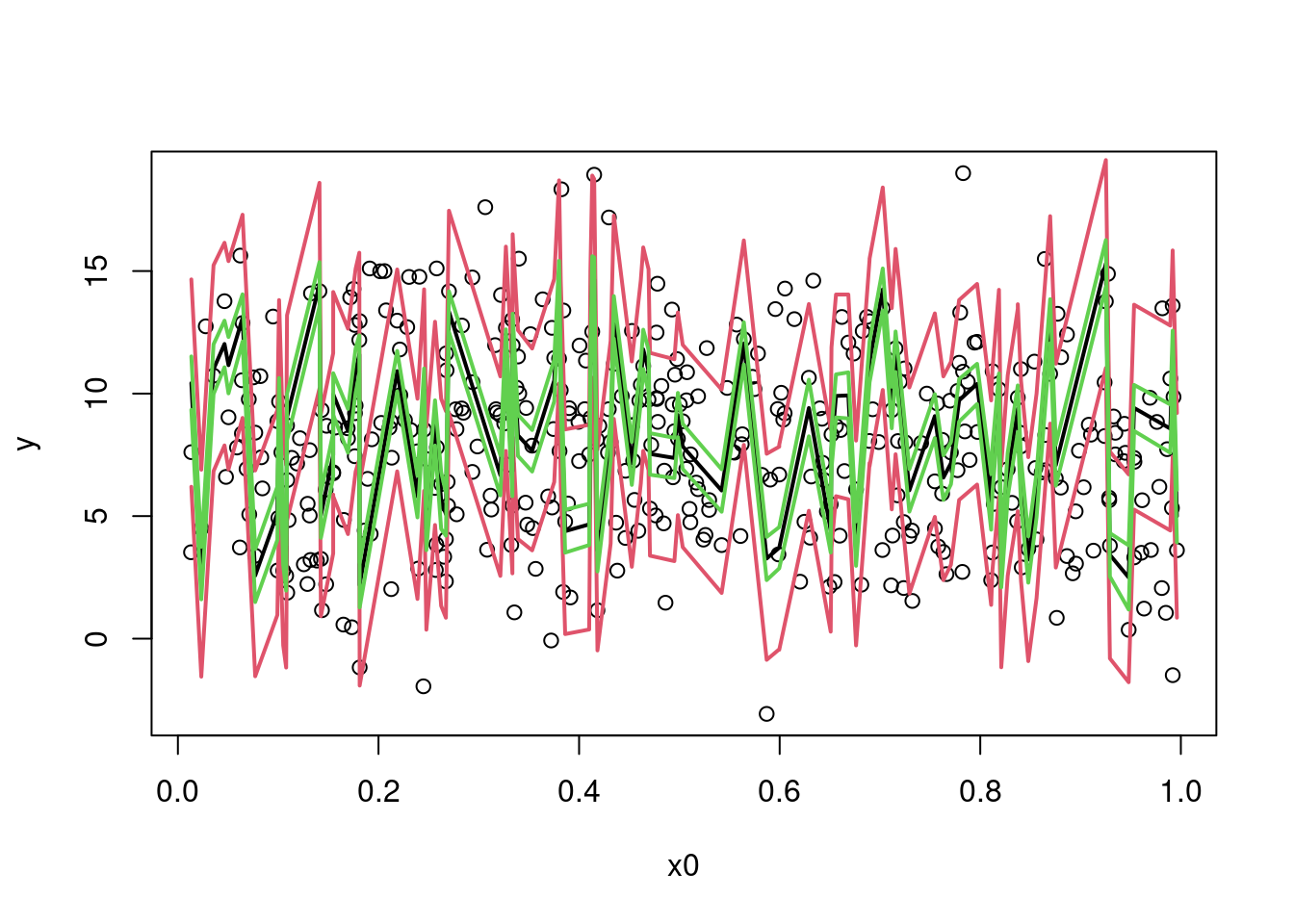
Confidence intervals can be added:

plot(y ~ x0, data = dat)

sim_dat_x0ord <- order(sim_dat$x0)
lines(sim_dat$x0[sim_dat_x0ord], pred_int_sim[1L, sim_dat_x0ord], col = 2, lwd = 2)
lines(sim_dat$x0[sim_dat_x0ord], pred_int_sim[2L, sim_dat_x0ord], col = 2, lwd = 2)

sim_dat_pred <- predict(fit_gam, newdata = sim_dat, se = TRUE)
lines(sim_dat$x0[sim_dat_x0ord], sim_dat_pred$fit[sim_dat_x0ord], col = 1, lwd = 2)

upr_ci <- invlink(sim_dat_pred$fit + 2*sim_dat_pred$se.fit)
lwr_ci <- invlink(sim_dat_pred$fit - 2*sim_dat_pred$se.fit)
lines(sim_dat$x0[sim_dat_x0ord], upr_ci[sim_dat_x0ord], col = 3, lwd = 2)
lines(sim_dat$x0[sim_dat_x0ord], lwr_ci[sim_dat_x0ord], col = 3, lwd = 2)