It is often very useful to practise mathematics by automatically generated exercises.
One approach is multiple choice quizzes (MCQ), but it turns out to be
fairly difficult to generate authentic wrong answers.
Instead, we want the user to input the answer and be able to parse the answer and check
whether this is the correct answer.
There are many fun challenges in this, e.g. to verify that 2 is equal to 1 + 1
(as text strings the two are different, but mathematically they are equal, at least to a convenient approximation in this case).
In this post I will demonstrate how to use R package Ryacas (computer algebra system, CAS) and the R package iomath under development (as well as shiny) to make a small, powerful Shiny app.
The resulting app is available at https://github.com/r-cas/shinymathexample.
First I will show the app, and then I will show a few central lines of code.
The shinymathexample app
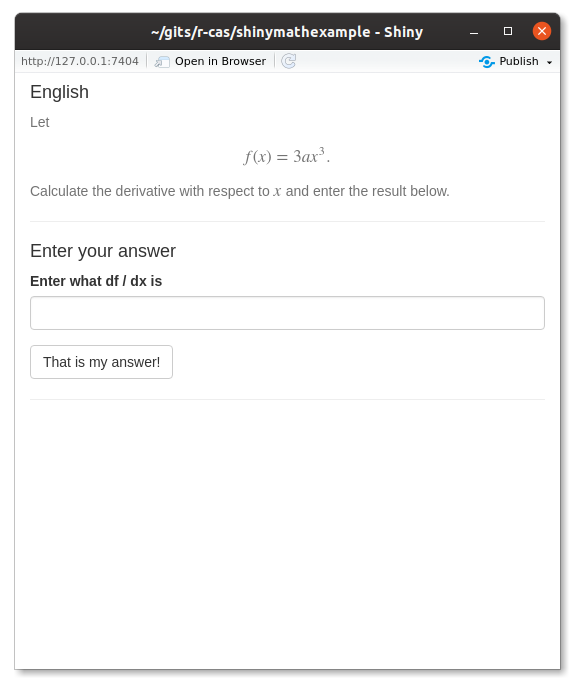
First, the shinymathexample app
presents the question:
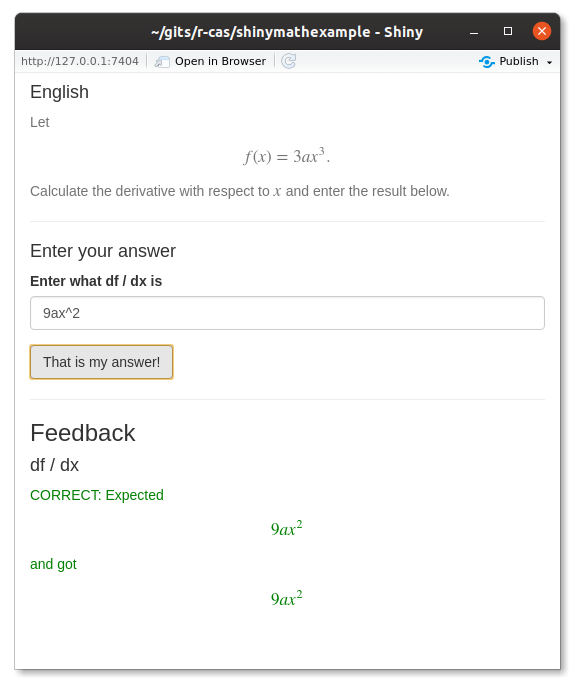
The answer can the be written and checked:
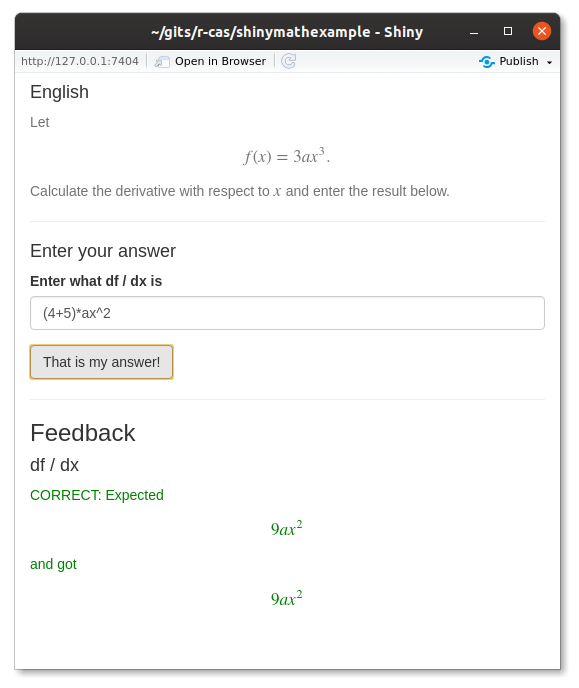
It even works for mathematical/numerical equality, not just text/string equality:
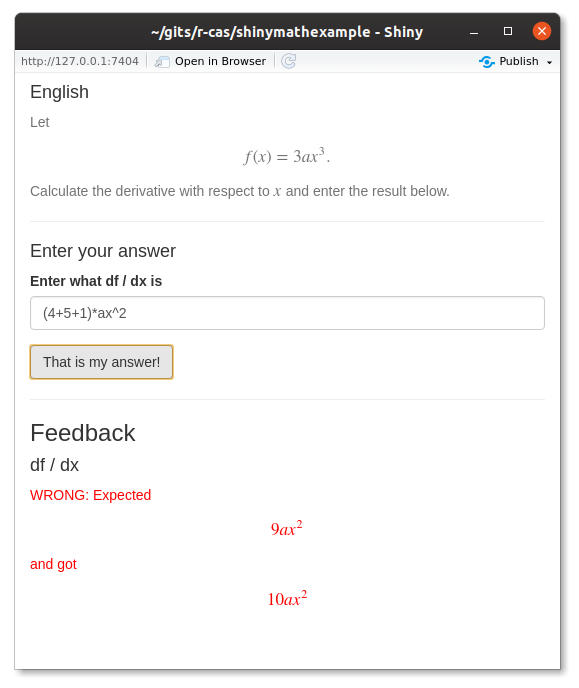
Finally wrong answers are caught, too:
Exercise generation
The exercise generation code (boiled down) is something like this:
choices_x_coef <- c("a", "2*a", "3*a")
choices_x_pow <- 1:3
generate_f <- function() {
x_coef <- sample(choices_x_coef, 1)
x_pow <- sample(choices_x_pow, 1)
x_part <- paste0(x_coef, "*x^", x_pow)
eq <- ysym(x_part)
eq
}
problem_f_eq <- generate_f()
true_ans <- list(
x = deriv(problem_f_eq, "x")
)
output$problem <- renderUI({
problem <- paste0("Let $$f(x) = ", tex(problem_f_eq), ".$$",
"Calculate the derivative with respect ",
"to \\(x\\) and enter the result below.")
res <- withMathJax(
helpText(problem)
)
return(res)
})Validation
The validation code (boiled down) is something like this:
reply <- input$answer_x
parsed_input <- iomath::prepare_input(reply)
if (inherits(parsed_input, "error")) {
stop("Could not prepare the input (remember that I'm simple-minded!).")
}
reply_sym <- tryCatch(Ryacas::ysym(parsed_input),
error = function(e) e)
if (inherits(reply_sym, "error")) {
stop("Could not understand the input (remember that I'm simple-minded!).")
}
compare_grid <- expand.grid(
x = seq(-10, 10, len = 6),
a = seq(-10, 10, len = 6)
)
is_correct <- tryCatch(iomath::compare_reply_answer(reply = reply,
answer = true_ans$x,
compare_grid = compare_grid),
error = function(e) e)
if (inherits(is_correct, "error")) {
stop(paste0("Error: ", is_correct$message))
}
is_correct # TRUE/FALSERemarks
Take a look at the complete code at https://github.com/r-cas/shinymathexample.
The provided example should illustrate that it is fairly easy to make something relatively sophisticated.
Beside the central aspect of Ryacas (e.g. for derivatives etc.), iomath has the important function compare_reply_answer that
compares reply to answer over the grid of values defined by compare_grid.
Thus, equality of expressions are measured as point-wise equality over a finite number of points (e.g. 100) for different values of variables including an allowed tolerance.