Korrelation er ikke transitiv

Er korrelation transitiv?

Lad \(\rho_{XY}\) være korrelationen mellem de stokastiske variable \(X\) og \(Y\), og tilsvarende for \(\rho_{XZ}\) samt \(\rho_{YZ}\). Spørgsmålet er så: Hvis vi kender to af disse korrelationer, hvad kan vi så sige om den tredje? Og i relation til DRs artikel: hvis to af dem er positive er den sidste så også positiv?²

Lad os antage, at vi kender de to korrelationer \(\rho_{XZ}\) og \(\rho_{YZ}\), og at vi vil udtale os om \(\rho_{XY}\). For at undersøge denne korrelation nærmere kan vi bruge begrebet partiel korrelation, der er korrelationen af \(X\) og \(Y\) givet \(Z\): \[ \rho_{XY \mid Z}={\frac {\rho_{XY}-\rho _{XZ}\rho_{YZ}}{{\sqrt {1-\rho_{XZ}^{2}}}{\sqrt {1-\rho_{YZ}^{2}}}}}. \]

Sagt på en anden måde, så betyder den partielle korrelation af \(X\) og \(Y\) givet \(Z\), at man udregner korrelationen mellem \(X\) og \(Y\) med effekten af \(Z\) fjernet. Formlen kan omskrives så man får et udtryk for den ukendte \(\rho_{XY}\):

\[\begin{align} \rho_{XY} &= \left( \rho_{XY \mid Z} - \frac{ - \rho_{XZ} \rho_{YZ}}{\sqrt{1 - \rho_{XZ}^{2}} \sqrt{1 - \rho_{YZ}^{2}}} \right) \sqrt{1 - \rho_{XZ}^{2}} \sqrt{1 - \rho_{YZ}^{2}} \\ &= \rho_{XY \mid Z} \sqrt{1 - \rho_{XZ}^{2}} \sqrt{1 - \rho_{YZ}^{2}} + \rho_{XZ} \rho_{YZ} \end{align}\]

Da \(\rho_{XY \mid Z}\) er en partiel korrelation vil den - ligesom den almindelige korrelation - antage værdier mellem \(-1\) og \(1\). Det betyder, at \(\rho_{XY}\) må ligge i intervallet \[ \rho_{XZ} \rho_{YZ} \pm \sqrt{1 - \rho_{XZ}^{2}} \sqrt{1 - \rho_{YZ}^{2}} . \]

Resultatet svarer til enhedscirklens ligning, og man får derfor, at informationen om fortegnet på \(\rho_{XY}\) (og dermed også sammenhængen mellem \(X\) og \(Y\)) som funktion af \(\rho_{XZ}\) og \(\rho_{YZ}\) kan illustreres ved enhedscirklen:

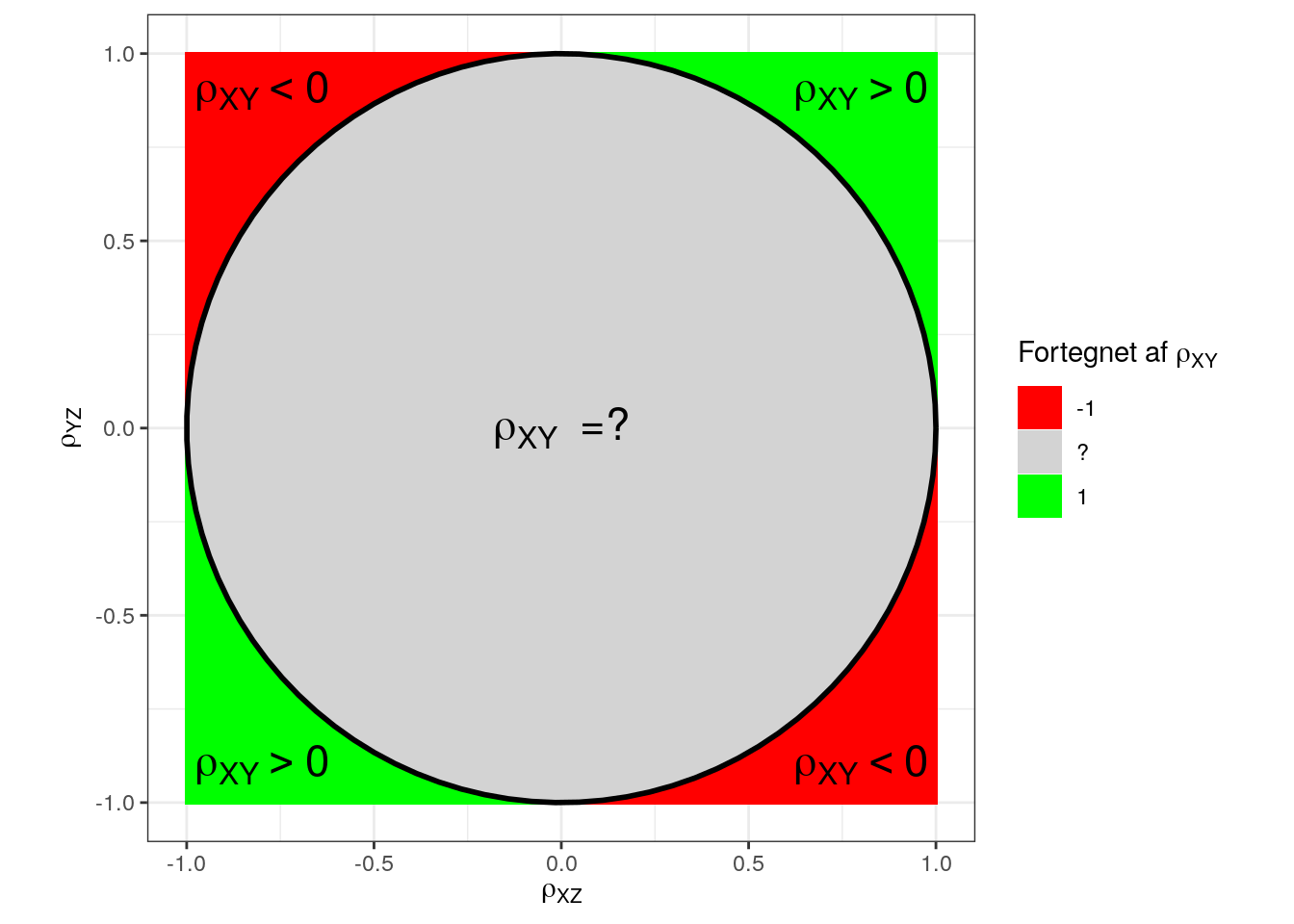
Figure 1: Fortegnet på korrelationen af \(\rho_{XY}\), når man kender \(\rho_{XZ}\) og \(\rho_{YZ}\). Når både \(\rho_{XZ}\) og \(\rho_{YZ}\) er kraftigt positivt korrelerede, så vil \(\rho_{XY}\) også være positivt korrelerede. Tilsvarende, hvis \(\rho_{XZ}\) og \(\rho_{YZ}\) begge er kraftigt negativt korrelerede. Når korrelationerne ikke er kraftige, kan vi ikke sige noget generelt om, hvad sammenhængen mellem \(X\) og \(Y\) bliver. Vi kan ikke engang være sikker på, hvilken retning sammenhængen har.

Nedenfor er vist et eksempel, hvor “mavefornemmelsen” (transitiviteten) går galt, og hvor to positive korrelationer alligevel resulterer i, at den tredie korrelation bliver negativ.

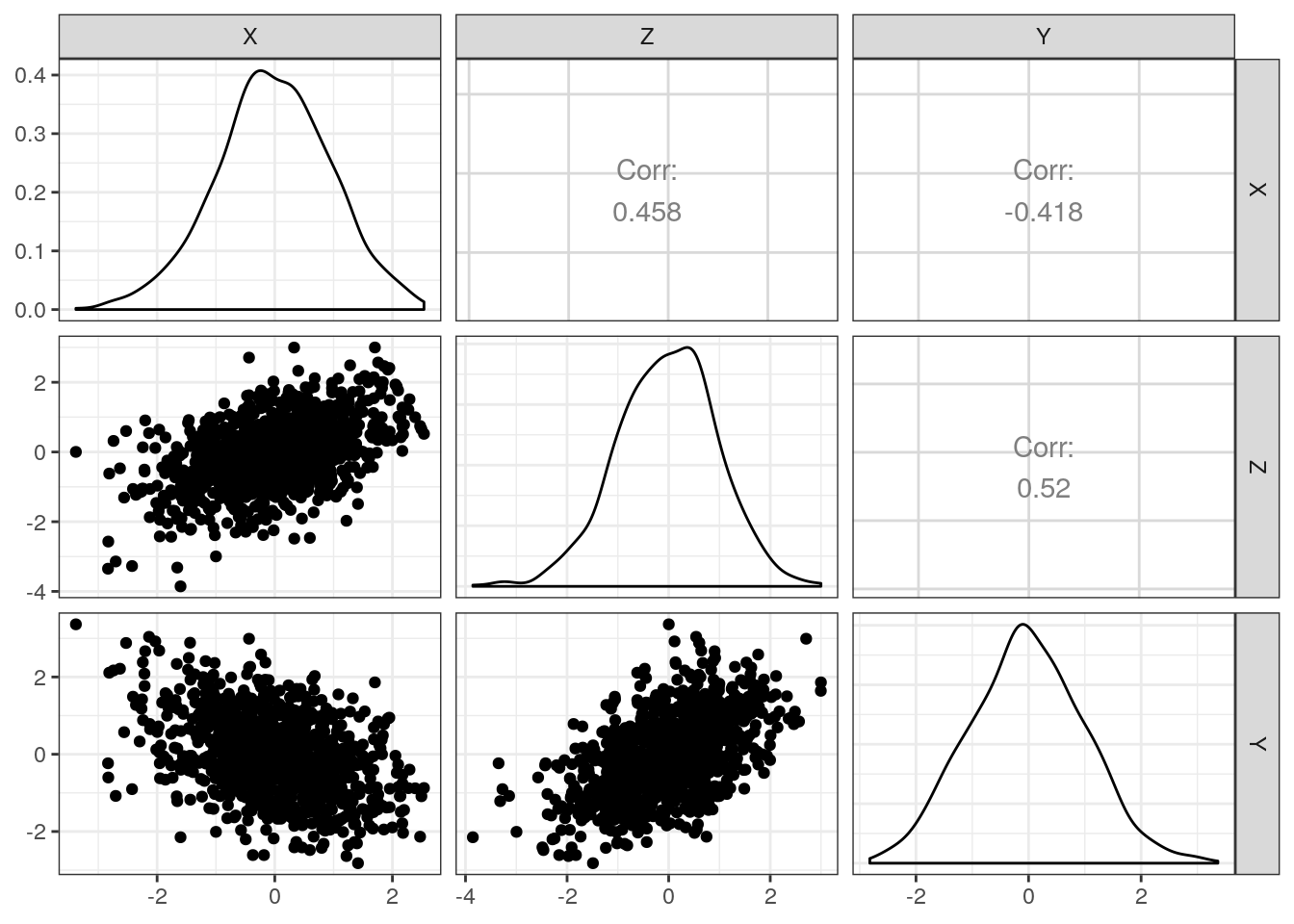
Figure 2: Eksempel, hvor \(\rho_{XZ}\) og \(\rho_{YZ}\) begge er positivt korrelerede med korrelationer på henholdsvis 0.46 og 0.52. Alligevel bliver korrelationen mellem \(X\) or \(Y\) til \(\rho_{XY}=-0.42\), der indikerer en negativ sammenhæng.

Som svar på spørgsmålet har vi her vist, at korrelationen ikke generelt er transitiv. Kun når de enkelte korrelationer er meget høje, kan man slutte, at den tredje korrelation med sikkerhed er positiv (og tilsvarende for lave og skiftende fortegn: de enkelte korrelationers numeriske værdi skal være tæt på 1 for at kunne sige noget generelt).

Er mobning så associeret til øget risiko for blodpropper i hjernen?

DRs artikel påstår, at mobning er positivt korreleret med risikoen for blodpropper i hjertet og hjernen fordi mobning er positivt korreleret med CRP, og fordi CRP er positivt korreleret med risikoen for blodpropper i hjertet og hjernen.

Det norske studie fandt en korrelation på omkring 0.2 mellem CRP og risikoen for blodpropper i hjertet og hjernen. Det betyder, at for at være sikker på, at der er en positiv korrelation mellem mobning og risikoen for blodpropper, så skal korrelationen mellem mobning og forhøjet CRP-niveau være \(\sqrt{1-0.2^2} \approx 0.98\), hvilket også fremgår af figur 1 ovenfor. Det er helt urealistisk, at korrelationen skulle være så høj mellem mobning og forhøjet CRP (og det finder studiet heller ikke), og konklusionen må derfor være, at man ikke bare kan konkludere, at mobning fører til øget risiko for blodpropper i hjertet og hjernen som DR gør ud fra de to studier.

Det betyder ikke nødvendigvis, at mobning og risiko for blodpropper i hjertet og hjernen ikke kunne være positivt korrelerede - det betyder bare at man ikke kan drage konklusionen udelukkende ud fra de to opgivne sammenhænge.

Det amerikanske studie fandt en effektstørrelse på 0.02, dvs. at man forventer, at CRP-niveauet i gennemsnit øges med 0.02 mg/L for mobbeofre i forhold til ikke-mobbeofre. Studiet selv opgiver median CRP (mg/L) til 0.75 for voksne, og med andre ord ser effekten af mobning altså ganske lille ud. Den er måske nok statistisk signifikant, men næppe biologisk relevant. Desuden beskriver det amerikanske studie sammenhængen mellem mobning og CRP blandt unge op til 21 år, mens det norske studie beskriver sammenhængen mellem 50+-årige og risikoen for blodpropper. Hvad der sker med CRP-niveauet mellem 21 og 50 er slet ikke undersøgt, og det vides ikke, og de personer, der har forhøjet CRP-niveau ved alder 21 også er dem, der har forhøjet CRP-niveau ved 50-års-alderen.